题目内容
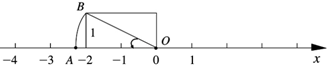
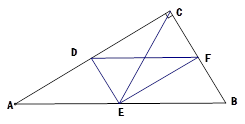
(本题满分7分)如图,已知在Rt△ABC,AB=AC,∠BAC=90°,过A的任一条直线AN,BD⊥AN于D,CE⊥AN于E。
⑴求证:DE=BD-CE
⑵如将直线AN绕A点沿顺时针方向旋转,使它不经过△ABC的内部,再作BD⊥AN于D,CE⊥AN于E,那么DE、DB、CE之间存在等量关系吗?若存在,请证明你的结论?

⑴求证:DE=BD-CE
⑵如将直线AN绕A点沿顺时针方向旋转,使它不经过△ABC的内部,再作BD⊥AN于D,CE⊥AN于E,那么DE、DB、CE之间存在等量关系吗?若存在,请证明你的结论?


(1)证明:∵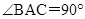 ,,BD⊥AN,∴
,,BD⊥AN,∴ ,
,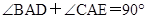 ,∴
,∴ ,∵BD⊥AN,CE⊥AN,∴
,∵BD⊥AN,CE⊥AN,∴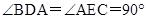 ,在△ABD与△CAE中,
,在△ABD与△CAE中,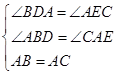 ,∴△ABD≌△CAE,∴
,∴△ABD≌△CAE,∴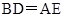 ,
,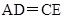 ,∵
,∵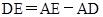 ,∴
,∴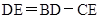
(2)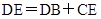
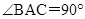 ,,BD⊥AN,∴
,,BD⊥AN,∴ ,
,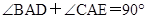 ,∴
,∴ ,∵BD⊥AN,CE⊥AN,∴
,∵BD⊥AN,CE⊥AN,∴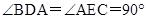 ,在△ABD与△CAE中,
,在△ABD与△CAE中,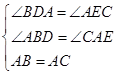 ,∴△ABD≌△CAE,∴
,∴△ABD≌△CAE,∴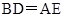 ,
,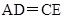 ,∵
,∵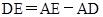 ,∴
,∴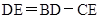
(2)
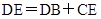
试题分析:(1)先通过证明三角形全等,从而证明
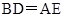 ,
,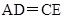 ,所以
,所以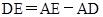 ,等量代换,可得
,等量代换,可得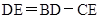
(2)∵BD⊥AN,CE⊥AN,∴
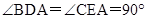 ,∴
,∴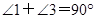 ,∵
,∵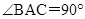 ,∴
,∴ ,∴
,∴ ,在△BDA和△AEC中,
,在△BDA和△AEC中,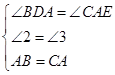 ,∴△BDA≌△AEC,∴
,∴△BDA≌△AEC,∴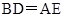 ,
,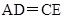 ,∴
,∴
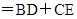
点评:本题难度一般,通过全等三角形的性质,证明两个三角形全等,进而证明对应边相等。全等三角形是考试必考部分,学生做此类题目时需要谨慎小心,依据全等三角形的各类判定依据进行推导

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
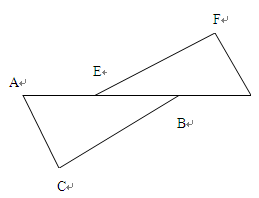

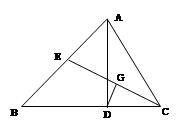
 ,且DE交△ABC外角
,且DE交△ABC外角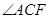 的平分线CE于点E,求证:AD=DE.
的平分线CE于点E,求证:AD=DE.

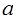 为偶数,且
为偶数,且 ,则这个三角形的周长为_______________。
,则这个三角形的周长为_______________。