题目内容
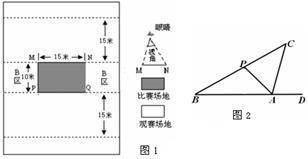
如图,已知∠AOB=80°,在射线OA、OB上分别取OA= OB1,连结AB1,在AB1、B1B上分别取点A1、B2,使A1 B1= B1 B2 ,连结A1 B2 …,按此规律下去,记∠A1 B1 B2=θ1 ,∠A2B2B3 =θ2, …,∠AnBnBn+1 =θn ,则θ2= ;θ2013= .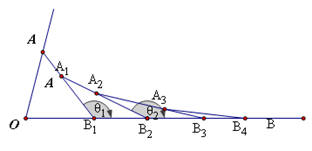

155° ; ((22013-1).180o+80o)/ 22013
试题分析:已知∠AOB=80°OA= OB1,所以∠OAB1=∠OB1A=50°,所以θ1=∠OAB1+∠AOB=130°。又因为A1 B1= B1 B2,∠B1A1B2=∠A1B2 B1=25°。所以θ2=θ1+∠B1A1B2=155°。
∴
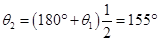 。
。∴
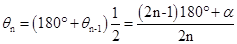
所以θ2013=
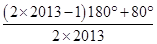
点评:本题难度较大。主要涉及外角的性质。需要用列举法列举一定例子来归纳总结一般式。

练习册系列答案
相关题目
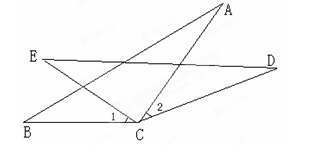
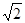 ,
,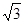 ,
,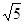
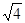 ,
,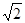 ,
,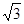
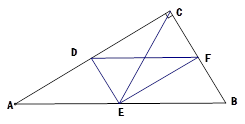
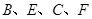 在同一直线上,
在同一直线上, ∥
∥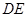 ,且
,且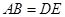 ,
,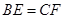 ,求证:
,求证: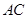 ∥
∥ .
.