题目内容
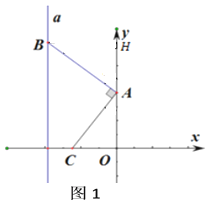
【题目】如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画一个格点△DEF,使△DEF ∽△ABC,且相似比为2∶1;
(2)求∠D的正弦值;
(3)若△ABC外接圆的圆心为P,则点P的坐标为__________.

【答案】(2,6)
【解析】
(1)利用相似比为2:1,将三角形各边扩大2倍,进而得出对应点位置即可得出答案;
(2)作FG⊥DE于G,在Rt△DFG中利用正弦函数的定义即可求解;
(3)设点P的坐标为(x,y),根据“三角形外接圆的圆心到三角形三个顶点的距离相等”列出等式,化简即可得出点P的坐标.
(1)如图所示:△DEF即为所求;
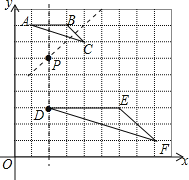
(2)如图,作FG⊥DE于G,
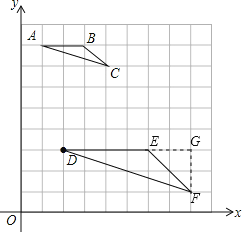
∵在Rt△DFG中,FG=2,DG=6,
∴DF=![]() ,
,
∴sin∠D=![]() ;
;
(3)设点P的坐标为(x,y);
∵△ABC外接圆的圆心为P,
∴PA=PB=PC,
∵A(1,8),B(3,8),C(4,7),
∴(1-x)2+(8-y)2=(3-x)2+(8-y)2=(4-x)2+(7-y)2,
化简后得x=2,y=6,
因此点P的坐标为(2,6).
故答案为(2,6).

 教学练新同步练习系列答案
教学练新同步练习系列答案【题目】某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |
(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?