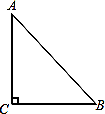Question

【题目】如图所示，AD、BE分别是钝角三角形ABC的边BC、AC上的高．

求证： =

Answer 1

【答案】证明： AD、BE分别是钝角三角形ABC的边BC、AC上的高

在△ACD中 同理 在△BCE中 ，

又 对顶角相等，

△ACD∽△BCE

，得证

【解析】根据求证得比例式可知要证△ACD∽△BCE ，题中隐含条件是对顶角相等，再由三角形的高得出一组角相等，即可证出结论。
【考点精析】本题主要考查了三角形的“三线”和相似三角形的判定与性质的相关知识点，需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．