题目内容
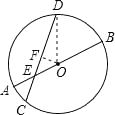
【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
【答案】解:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA﹣AE=4﹣2=2,
在Rt△OEF中,∠DEB=30°,
∴OF= ![]() OE=1,
OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF= ![]() =
= ![]() ,
,
则CD=2DF=2 ![]() .
.
【解析】过O作OF⊥CD,交CD于点F,连接OD,根据垂径定理求出CF=DF,根据AE=2,EB=6,易求出OE的长,根据直角三角形中30°角所对的直角边等于斜边的一半,求出OF的长,在Rt△ODF中,利用勾股定理即可求出CD的长。
【考点精析】根据题目的已知条件,利用含30度角的直角三角形和勾股定理的概念的相关知识可以得到问题的答案,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目