Question

【题目】在⊙O中，AB为⊙O的直径，AC是弦， ， ．
（1）在图1中，P为直径BA延长线上的一点，当CP与⊙O相切时，求PO的长；

（2）如图2，一动点M从A点出发，在⊙O上按逆时针方向运动一周，当 时，求半径OM所扫过的扇形的面积．

Answer 1

【答案】
（1）解：∵CP与⊙O相切，OC是半径．

∴CP⊥OC，

又∵∠OAC=∠AOC=60°，

∴∠P=90°-∠AOC=30°，

∴在Rt△POC中，CO= PO=4，

则PO=2CO=8

（2）解：如图，

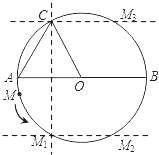
①作点C关于直径AB的对称点M1，连接AM1，OM1．

易得S△M1AO=S△CAO，∠AOM1=60°∴当点M运动到M1时，S△MAO=S△CAO，

此时点M经过的弧长为 ，

∴半径OM所扫过的扇形的面积= ；

②过点M1作M1M2∥AB交⊙O于点M2，连接AM2，OM2，易得S△M2AO=S△CAO．

∴∠AOM1=∠M1OM2=∠BOM2=60°

∴ 或 ，

∴当点M运动到M2时，S△MAO=S△CAO，此时点M经过的弧长为 ，

∴半径OM所扫过的扇形的面积= × ×4= π；

③过点C作CM3∥AB交⊙O于点M3，连接AM3，OM3，易得S△M3AO=S△CAO

∴∠BOM3=60°，

∴ = ×240或 = ×2=

∴当点M运动到M3时，S△MAO=S△CAO，此时点M经过的弧长为 ，

∴半径OM所扫过的扇形的面积= × ×4= ；

④当点M运动到C时，M与C重合，S△MAO=S△CAO，

此时点M经过的弧长为 ×300°或 π+ =

∴半径OM所扫过的扇形的面积= × ×4=

【解析】（1）根据CP与⊙O相切，得出CP⊥OC，根据题意易证△OAC是等边三角形，可求出∠P=30°，再根据直角三角形中，30°的直角边等于斜边的一半，求出OP的长。
（2）如图，当S△MAO=S△CAO时，动点M的位置有四种．①作点C关于直径AB的对称点M1，连接AM1，OM1，先证S△MAO=S△CAO，再求出点M经过的弧长，即可求出半径OM所扫过的扇形的面积；②过点M1作M1M2∥AB交 O于点M2，连接AM2，OM2，③过点C作CM3∥AB交 O于点M3，连接AM3，OM3；④当点M运动到C时，M与C重合，求得每种情况的OM转过的度数，再根据弧长公式求得点M经过的弧长，然后求出半径OM所扫过的扇形的面积。
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识，掌握在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．