题目内容
【题目】抛物线![]() 经过点E(5,5),其顶点为C点.
经过点E(5,5),其顶点为C点.
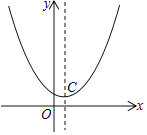
(1)求抛物线的解析式,并直接写出C点坐标.
(2)将直线![]() 沿y轴向上平移b个单位长度交抛物线于A、B两点.若∠ACB=90°,求b的值.
沿y轴向上平移b个单位长度交抛物线于A、B两点.若∠ACB=90°,求b的值.
(3)是否存在点D(1,a),使抛物线上任意一点P到x轴的距离等于P点到点D的距离?若存在,请求点D的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ,顶点(1,1)(2)
,顶点(1,1)(2)![]() (3)(1,2)
(3)(1,2)
【解析】
(1)将点E坐标代入解析式,求出系数a,获得解析式,并求出顶点C坐标;
(2)平移直线y=![]() ,获得平移后的解析式y=
,获得平移后的解析式y=![]() ,直线与抛物线交于两点A、B,设A(x1,y1)、B(x2,y2),因为∠ACB=90°,利用A、B、C三点构造相似,得到
,直线与抛物线交于两点A、B,设A(x1,y1)、B(x2,y2),因为∠ACB=90°,利用A、B、C三点构造相似,得到![]()
![]() ,将直线与抛物线联立获得方程,根据韦达定理,获得x1+x2,x1x2,从而获得关于b的方程,求出b值;
,将直线与抛物线联立获得方程,根据韦达定理,获得x1+x2,x1x2,从而获得关于b的方程,求出b值;
(3)过点P作PQ⊥x轴,设点P(m,![]() )因为PQ=PD,所以PQ2=PD2,整理可得
)因为PQ=PD,所以PQ2=PD2,整理可得![]() ,所以当a=2时,存在点D(1,2).
,所以当a=2时,存在点D(1,2).
(1)将点E(5,5)代入y=ax2-![]() +
+![]()
5=25a-![]() +
+![]()
a=![]()
∴y=![]() ,顶点(1,1)
,顶点(1,1)
(2)直线y=![]() 平移后获得解析式y=
平移后获得解析式y=![]()
交抛物线于A(x1,y1)、B(x2,y2)
y1=![]() ,y2=
,y2=![]()
联立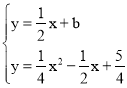
x2-4x+5-4b=0
∴x1+x2=4,x1x2=5-4b
如图,过点A、B作y轴的平行线与过点C平行于x轴的线交于点E,F
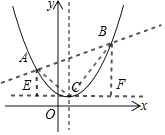
可证△ACE∽△BCF
∴![]() =
=![]()
∴(x1+x2)-(x1x2)-1=y1y2-(y1+y2)+1
∴b2-5b+![]() =0,
=0,
解,b1=![]() ,b2=
,b2=![]() (舍)
(舍)
∴b=![]() .
.
(3)设P(m,n),作PQ⊥x轴于Q
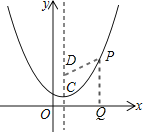
若PQ=PD,则PQ2=PD2
(m-1)2+(n-a)2=n2
整理得
m2-2m+1+a2-2an=0
将n=![]() 代入
代入
整理得![]()
当a=2时,方程成立
∴D(1,2)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目