Question

【题目】对于平面直角坐标系xOy中的点P和直线m，给出如下定义：若存在一点P，使得点P到直线m的距离等于1，则称P为直线m的平行点．

（1）当直线m的表达式为y＝x时，

①在点，，中，直线m的平行点是______；

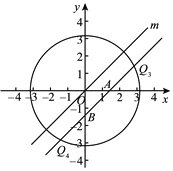
②⊙O的半径为，点Q在⊙O上，若点Q为直线m的平行点，求点Q的坐标．

（2）点A的坐标为（n，0），⊙A半径等于1，若⊙A上存在直线的平行点，直接写出n的取值范围．

Answer 1

【答案】（1）①，;②，，，;（2）．

【解析】

(1)①根据平行点的定义即可判断；

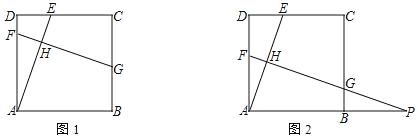
②分两种情形：如图1，当点B在原点上方时，作OH⊥AB于点H，可知OH=1.如图2，当点B在原点下方时，同法可求；

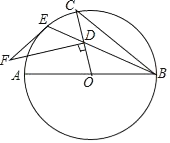
(2)如图，直线OE的解析式为，设直线BC//OE交x轴于C，作CD⊥OE于D. 设⊙A与直线BC相切于点F，想办法求出点A的坐标，再根据对称性求出左侧点A的坐标即可解决问题；

解：（1）①因为P2、P3到直线y＝x的距离为1，

所以根据平行点的定义可知，直线m的平行点是，，

故答案为，．

②解：由题意可知，直线m的所有平行点组成平行于直线m，且到直线m的距离为1的直线．

设该直线与x轴交于点A，与y轴交于点B．

如图1，当点B在原点上方时，作OH⊥AB于点H，可知OH＝1．

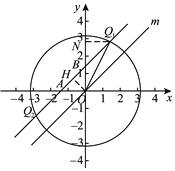
由直线m的表达式为y＝x，可知∠OAB＝∠OBA＝45°．

所以．

直线AB与⊙O的交点即为满足条件的点Q．

连接，作轴于点N，可知．

在中，可求．

所以．

在中，可求．

所以．

所以点的坐标为．

同理可求点的坐标为．

如图2，当点B在原点下方时，可求点的坐标为点的坐标为，

综上所述，点Q的坐标为，，，．

（2）如图，直线OE的解析式为，设直线BC∥OE交x轴于C，作CD⊥OE于D．

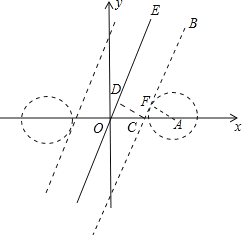
当CD＝1时，在Rt△COD中，∠COD＝60°，

∴，

设⊙A与直线BC相切于点F，

在Rt△ACE中，同法可得，

∴，

∴，

根据对称性可知，当⊙A在y轴左侧时，，

观察图象可知满足条件的N的值为：．