题目内容
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为BC边上的一个动点(不与点B,C重合).点P关于直线AC,AB的对称点分别为M,N,连接MN交AC于点E,交AB于点F.
(1)当点P为线段BC的中点时,求∠M的正切值.
(2)当点P在线段BC上运动时(不与B,C重合),连接AM,AN,求证:
①△AMN为等腰直角三角形;
②△AEF∽△BAM.

【答案】(1)![]() ;(2)①见解析;②见解析.
;(2)①见解析;②见解析.
【解析】
(1)连接NB,根据对称的性质可证明BP=BN,进而证明∠MBN=90°,根据P为中点可证明MC=CP=PB=NB=1,求出∠M的正切值即可;(2)①如图:连接AP,根据对称性质可知AP=AM=AN,∠1=∠2,∠3=∠4,由∠CAB=∠2+∠3=45°证明∠MAN=90即可;②由∠AEF=∠5+∠1=45°+∠1,∠BAM=∠EAF+∠1=45°+∠1,可知∠AEF=∠BAM,再根据∠B==∠EAF=45°,即可证明△AEF∽△BAM.
(1)连接NB.
∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠A=∠CBA=45°.
∵点P关于直线AB的对称点为N,关于直线AC的对称点为M,
∴AB垂直PN,BN=BP,
∴∠NBA=∠PBA=45°,
∴∠PBN=90°,
∵P为BC的中点,BC=2,∴MC=CP=PB=NB=1,
∴tan ∠M=![]() .
.
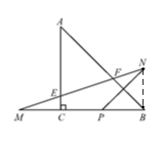
(2)①连接AP,如图.
∵点P关于直线AC,AB的对称点分别为M,N,
∴AP=AM=AN,∠1=∠2,∠3=∠4,
∵∠CAB=∠2+∠3=45°,
∴∠MAN=90°,
∴△AMN为等腰直角三角形.
②∵△AMN为等腰直角三角形,
∴∠5=∠6=45°,
∴∠AEF=∠5+∠1=45°+∠1,
∵∠EAF=45°,
∴∠BAM=∠EAF+∠1=45°+∠1,
∴∠AEF=∠BAM,
又∵∠B=∠BAC=45°,
∴△AEF∽△BAM.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案【题目】在《朗读者》节目的影响下,某中学开展了“好书伴我成长”读书活动.为了解5月份八年级300名学生的读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
关于这组数据,下列说法正确的是 ( )
A. 中位数是2 B. 众数是17 C. 平均数是3 D. 方差是2




