题目内容
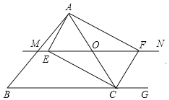
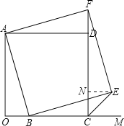
【题目】如图,正方形![]() 中,点
中,点![]() 是
是![]() 上任意一点,以
上任意一点,以![]() 为边作正方形
为边作正方形![]() .
.
①连接![]() ,求证:
,求证:![]() ;
;
②连接![]() ,猜想
,猜想![]() 的度数,并证明你的结论;
的度数,并证明你的结论;
③设点![]() 在线段
在线段![]() 上运动,
上运动,![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,试求
,试求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.

【答案】(1)证明见解析;(2)![]() 的度数为
的度数为![]() ,证明见解析;(3)
,证明见解析;(3)![]() .
.
【解析】
(1)根据三角形全等的判定定理,可以证得△AOB≌△ADF,进而得出结论.
(2)过E作CD的垂线,得出所构成的三角形为等边三角形,继而得出所求角的度数为45°.
(3)由正方形AOCD的面积,可以而出边长,又有OB的长,根据勾股定理,得出正方形ABEF的边长,继而求出面积,在边OC上运动,则可得出x的取值范围.
![]() 证明:∵正方形
证明:∵正方形![]() ,
,
∴![]() ,
,![]() ,
,
∵正方形![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() 猜想
猜想![]() 的度数为
的度数为![]()
证明:如图,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
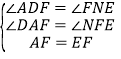 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴三角形![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() .
.
![]() 解:∵
解:∵![]() ,
,
∴![]() ,
,
∵正方形![]() 的面积为
的面积为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 在线段
在线段![]() 上运动,
上运动,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目