ĖâÄŋÄÚČÝ
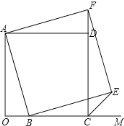
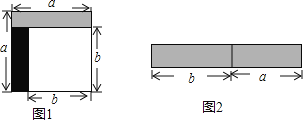
ĄūĖâÄŋĄŋīÓąßģĪΊaĩÄÕý·―ÐÎÖОôĩôŌŧļöąßģĪΊbĩÄÕý·―ÐÎĢĻČįÍž1ĢĐĢŽČŧšó―ŦĘĢÓāēŋ·ÖÆīģÉŌŧļöģĪ·―ÐÎĢĻČįÍž2ĢĐ.
ĢĻ1ĢĐÉÏĘöēŲŨũÄÜŅéÖĪĩÄĩČĘ―ĘĮ________ĢĻĖîAŧōBŧōCĢĐ
AĢŪa2-2ab+b2=ĢĻa-bĢĐ2
BĢŪa2-b2=ĢĻa+bĢĐĢĻa-bĢĐ
CĢŪa2+ab=aĢĻa+bĢĐĄĄĄĄ
ĢĻ2ĢĐÓĶÓÃÄãīÓĢĻ1ĢĐÖÐŅĄģöĩÄĩČĘ―ĢŽÍęģÉÏÂÁÐļũĖâĢš
ĒŲŌŅÖŠx2-4y2=12,x+2y=4,Įóx-2yĩÄÖĩ
ĒÚžÆËãĢšĢĻ1-![]() ĢĐĢĻ1-
ĢĐĢĻ1-![]() ĢĐĢĻ1-
ĢĐĢĻ1-![]() ĢĐĄĢĻ1-
ĢĐĄĢĻ1-![]() ĢĐĢĻ1-
ĢĐĢĻ1-![]() ĢĐ
ĢĐ
Ąūīð°ļĄŋĢĻ1ĢĐB;ĢĻ2ĢĐĒŲ3ĢŧĒÚ![]()
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝÍž1―ŦŌõÓ°ēŋ·ÖĩÄÃæŧýąíĘūģöĀīĢŽÔŲ―ŦÍž2ģĪ·―ÐÎÃæŧýąíĘūģöĀīĢŽžīŋÉĩÃģöĩČĘ―.
ĢĻ2ĢĐĒŲÔËÓÃĢĻ1ĢĐÖÐŅĄģöĩÄÆ―·―ēîđŦĘ―ĮóžīŋÉĢŧ
ĒÚ―ŦÃŋŌŧÏîÔËÓÃÆ―·―ēîđŦĘ―ēðģÉÁ―ÏîÏāģËĢŽ·ĒÏÖÖОäĩÄÏîŋÉŌÔĩÖÏûĢŽŨîšóÖŧĘĢÁ―ÏîÏāģËžīŋÉ.
ĢĻ1ĢĐļųūÝÍž1―ŦŌõÓ°ēŋ·ÖĩÄÃæŧýąíĘūģöĀīΊ![]() ĢŽČŧšó―ŦÍž2ĩÄģĪ·―ÐÎĩÄÃæŧýąíĘūģöĀīΊ
ĢŽČŧšó―ŦÍž2ĩÄģĪ·―ÐÎĩÄÃæŧýąíĘūģöĀīΊ![]() ĢŽžīŋÉĩÃĩ―ĩČĘ―
ĢŽžīŋÉĩÃĩ―ĩČĘ―![]()
ĢĻ2ĢĐĒŲ![]()
![]()
![]()
ĒÚÔĘ―=![]()
=![]()
=![]()
=![]()

Á·Ï°ēáÏĩÁÐīð°ļ
ÏāđØĖâÄŋ