题目内容
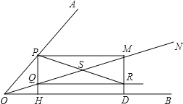
【题目】如图,![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,交
,交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 判断
判断![]() 与
与![]() 的大小关系?并说明理由;
的大小关系?并说明理由;
![]() 当点
当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并说出你的理由;
是矩形?并说出你的理由;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形.直接写出答案,不需说明理由.
是正方形.直接写出答案,不需说明理由.
【答案】(1)详见解析;(2)当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是矩形,理由详见解析;(3)当
是矩形,理由详见解析;(3)当![]() 是直角三角形时,即当
是直角三角形时,即当![]() 时,四边形
时,四边形![]() 会是正方形,理由详见解析.
会是正方形,理由详见解析.
【解析】
(1)利用平行线的性质得:∠OEC=∠ECB,根据角平分线的定义可知:∠ACE=∠ECB,由等量代换和等角对等边得:OE=OC,同理:OC=OF,可得结论;
(2)先根据对角线互相平分证明四边形AECF是平行四边形,再由角平分线可得:∠ECF=90°,利用有一个角是直角的平行四边形可得结论;
(3)由(2)可知,当点O为AC的中点时,四边形AECF是矩形,再证明AC⊥EF,即可得出答案.
![]() ∵
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可得:![]() ,
,
∴![]() ;
;
![]() 当
当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是矩形;
是矩形;
理由如下:
∵![]() ,
,![]() (已证),
(已证),
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴四边形![]() 是矩形;
是矩形;
![]() 当
当![]() 是直角三角形时,即当
是直角三角形时,即当![]() 时,四边形
时,四边形![]() 会是正方形;
会是正方形;
理由:由![]() 得,当点
得,当点![]() 为
为![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,
是矩形,
∵![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是正方形.
是正方形.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目