题目内容
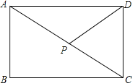
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上的动点(不与
上的动点(不与![]() 、
、![]() 重合),设
重合),设![]() ,
,![]() .
.
![]() 求
求![]() 与
与![]() 的函数解析式,并指出
的函数解析式,并指出![]() 的取值范围;
的取值范围;
![]() 连接
连接![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 是等腰三角形时,
是等腰三角形时,![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用勾股定理列式求出AC,再根据三角形的面积求出点D到AC的距离,然后表示出PC,再根据三角形的面积公式列式整理即可得解;
(2)分AP=AB=3;AP=BP时,由等腰三角形三线合一的性质可得点P在AB的垂直平分线上,此时AP=![]() AC;AB=BP时,利用∠BAC的余弦列式求出AP,然后分别代入函数关系式进行计算即可得解.
AC;AB=BP时,利用∠BAC的余弦列式求出AP,然后分别代入函数关系式进行计算即可得解.
解:![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
设点![]() 到
到![]() 的距离为
的距离为![]() ,
,
则![]() ,
,
解得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 时,
时,![]() ,
,![]() ;
;
![]() 时,点
时,点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,![]() ,
,
![]() ;
;
![]() 时,
时,![]() ,
,
![]() ,
,
综上所述,![]() 是等腰三角形时,
是等腰三角形时,![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目