题目内容
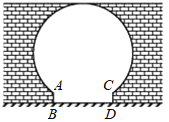
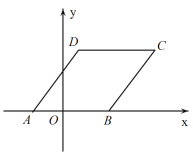
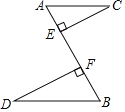
【题目】如图,两车从路段AB两端同时出发,沿平行路线行驶(即AC∥BD),CE和DF的长分别表示两车到道路AB的距离.
(1)如果两车行驶速度不相同,证明:△ACE∽△BDF;
(2)添加一个条件,使△ACE≌△BDF,请说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)直接利用平行线的性质以及相似三角形的判定方法进而得出答案;
(2)结合全等三角形的判定方法即可得出答案.
(1)证明:∵AC∥BD,
∴∠A=∠B,
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°,
∴△ACE∽△BDF;
(2) 由(1)可知△ACE∽△BDF;如果相似比是1,则△ACE≌△BDF,所以需要有一条边相等,
我们发现决定两个三角形边长变化的是AC和BD的长度,
所以只要AC=BD,则可满足△ACE≌△BDF;
那么要使AC=BD,由已知可知两车同时出发,所以两车速度相同则可以保证AC=BD,
所以添加两车等速行驶即可
证明:∵AC∥BD,
∴∠A=∠B,
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°,
∵两车等速同时行驶,
∴AC=BD,
在△ACE和△BDF中
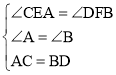 ,
,
∴△ACE≌△BDF(AAS).

练习册系列答案
相关题目
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次,平均数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.