题目内容
【题目】(本小题满分8分)
阅读材料：
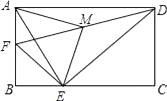
如图,在四边形ABCD中，对角线AC⊥BD，垂足为P.
求证：S四边形ABCD=
证明：AC⊥BD→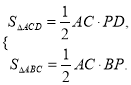
∴S四边形ABCD=S△ACD+S△ACB= 
=
解答问题：
（1）上述证明得到的性质可叙述为_______________________________________.
（2）已知：如图，等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD=3cm,BC=7cm，利用上述的性质求梯形的面积.
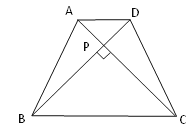
【答案】（1）对角线互相垂直的四边形的面积等于对角线乘积的一半. （2）S梯形=25(cm2).
【解析】试题分析：本题的关键是求出AC，BD的长，可过A，D分别作BC的垂线AE，DF，在直角三角形BFD中，可根据两底的差求出BE，CF的长，也就求出了BF，CE的长，要求BD还需知道直角三角形中一个锐角的度数，可通过全等三角形ACB和DBC得出∠DBC=∠ACB=45°，由此可得出BD，AC的长，进而根据题目给出的面积计算方法求出梯形的面积．
试题解析：（1）叙述：对角线互相垂直的四边形的面积等于对角线乘积的一半；
（2）过A，D分别作BC的垂线AE，DF，
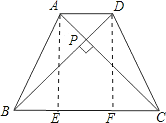
∵四边形ABCD为等腰梯形，
∵BD=AC，AB=CD，BC=BC
∴△ABC≌△DBC
∴∠ACB=∠DBC=45°，
在直角三角形BPC中，∠DBC=45°，BP=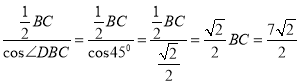
同理可得PD= 
，BD=BP+PD=5
．
又等腰梯形对角线相等，即BD=AC=5
cm
∴S梯形=
BDAC=25（cm2）；
练习册系列答案
相关题目
