题目内容
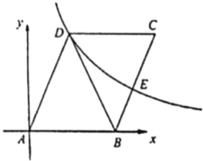
【题目】如图，四边形OABC是矩形，等腰△ODE中，OE＝DE，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点B、E在反比例函数y＝
的图象上，OA＝5，OC＝1，则△ODE的面积为（ ）
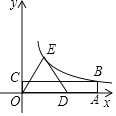
A.2.5B.5C.7.5D.10
【答案】B
【解析】
过E作EF⊥OC于F，由等腰三角形的性质得到OF＝DF，于是得到S△ODE＝2S△OEF，由于点B、E在反比例函数y＝
的图象上，于是得到S矩形ABCO＝k，S△OEF＝
k，即可得到结论．
解：
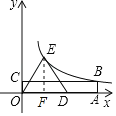
过E作EF⊥OD于F，
∵OE＝DE，
∴OF＝DF，
∴S△ODE＝2S△OEF，
∵点B、E在反比例函数y＝的图象上，
∴S矩形ABCO＝k，S△OEF＝k，
∴S△ODE＝S矩形ABCO＝5×1＝5，
故选：B．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】某兴趣小组对函数y＝
的图象和性质进行探究，请你帮助解决下面问题：
（1）函数y＝中自变量x的取值范围是 ；
（2）如表是x、y的几组对应值，则m＝ ；
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
（3）如图，已经画出了该函数图象的一部分，请你画出函数图象的另一部分；
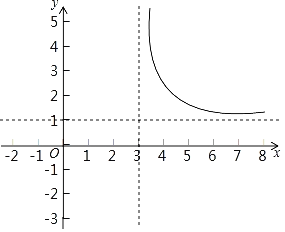
（4）该函数图象两个分支关于一个点成中心对称，这个点的坐标是 ；
（5）若函数y＝的图象上有三点A（x1，y1）、B（x2，y2）、C（x3，y3）且x1＜x2＜3＜x3，则y1、y2、y3的大小关系是 （用“＜”连接）．
