题目内容
【题目】已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否在直线y=4x+1上,并说明理由.
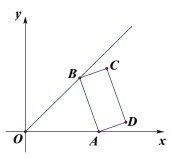
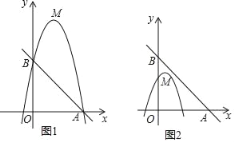
(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.
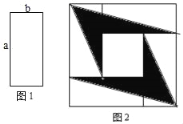
(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(![]() ,y1),D(
,y1),D(![]() ,y2)都在二次函数图象上,试比较y1与y2的大小.
,y2)都在二次函数图象上,试比较y1与y2的大小.
【答案】(1)点M在直线y=4x+1上;理由见解析;(2)x的取值范围是x<0或x>5;(3)①当0<b<![]() 时,y1>y2,②当b=
时,y1>y2,②当b=![]() 时,y1=y2,③当
时,y1=y2,③当![]() <b<
<b<![]() 时,y1<y2.
时,y1<y2.
【解析】
(1)根据顶点式解析式,可得顶点坐标,根据点的坐标代入函数解析式检验,可得答案;
(2)根据待定系数法,可得二次函数的解析式,根据函数图象与不等式的关系:图象在下方的函数值小,可得答案;
(3)根据解方程组,可得顶点M的纵坐标的范围,根据二次函数的性质,可得答案.
(1)点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,
∴M的坐标是(b,4b+1),
把x=b代入y=4x+1,得y=4b+1,
∴点M在直线y=4x+1上;
(2)如图1,
直线y=mx+5交y轴于点B,
∴B点坐标为(0,5)又B在抛物线上,
∴5=﹣(0﹣b)2+4b+1=5,解得b=2,
二次函数的解析是为y=﹣(x﹣2)2+9,
当y=0时,﹣(x﹣2)2+9=0,解得x1=5,x2=﹣1,
∴A(5,0).
由图象,得
当mx+5>﹣(x﹣b)2+4b+1时,x的取值范围是x<0或x>5;
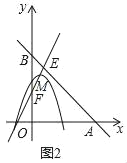
(3)如图2,
∵直线y=4x+1与直线AB交于点E,与y轴交于F,
A(5,0),B(0,5)得
直线AB的解析式为y=﹣x+5,
联立EF,AB得方程组![]() ,
,
解得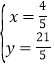 ,
,
∴点E(![]() ,
,![]() ),F(0,1).
),F(0,1).
点M在△AOB内,
1<4b+1<![]() ,
,
∴0<b<![]() .
.
当点C,D关于抛物线的对称轴对称时,b﹣![]() =
=![]() ﹣b,∴b=
﹣b,∴b=![]() ,
,
且二次函数图象开口向下,顶点M在直线y=4x+1上,
综上:①当0<b<![]() 时,y1>y2,
时,y1>y2,
②当b=![]() 时,y1=y2,
时,y1=y2,
③当![]() <b<
<b<![]() 时,y1<y2.
时,y1<y2.

 阅读快车系列答案
阅读快车系列答案