题目内容
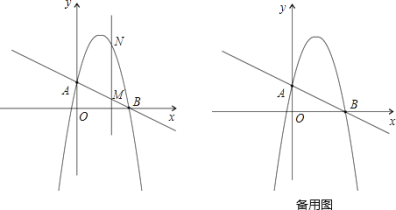
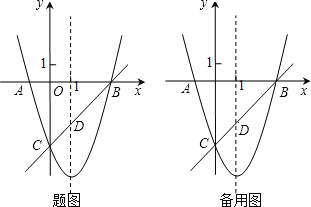
【题目】如图，已知抛物线y=x2＋bx＋c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，－3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．
（1）求抛物线的函数表达式；
（2）求直线BC的函数表达式；
（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．
①当线段PQ=
AB时，求tan∠CED的值；
②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．
【答案】（1）抛物线的函数表达式为y=x2－2x－3．（2）直线BC的函数表达式为y=x－3．（3）①
．①P1（1－
，－2），P2（1－
，
）．
【解析】
已知C点的坐标，即知道OC的长，可在直角三角形BOC中根据∠BCO的正切值求出OB的长，即可得出B点的坐标．已知了△AOC和△BOC的面积比，由于两三角形的高相等，因此面积比就是AO与OB的比．由此可求出OA的长，也就求出了A点的坐标，然后根据A、B、C三点的坐标即可用待定系数法求出抛物线的解析式．
（1）∵抛物线的对称轴为直线x=1，
∴
＝1
∴b=-2
∵抛物线与y轴交于点C（0，-3），
∴c=-3，
∴抛物线的函数表达式为y=x2-2x-3；
（2）∵抛物线与x轴交于A、B两点，
当y=0时，x2-2x-3=0．
∴x1=-1，x2=3．
∵A点在B点左侧，
∴A（-1，0），B（3，0）
设过点B（3，0）、C（0，-3）的直线的函数表达式为y=kx+m，
则
，
∴
∴直线BC的函数表达式为y=x-3；
（3）①∵AB=4，PQ=
AB，
∴PQ=3
∵PQ⊥y轴
∴PQ∥x轴，
则由抛物线的对称性可得PM=
，
∵对称轴是直线x=1，
∴P到y轴的距离是
，
∴点P的横坐标为，
∴P（，）
∴F（0，），
∴FC=3-OF=3-=
∵PQ垂直平分CE于点F，
∴CE=2FC=
∵点D在直线BC上，
∴当x=1时，y=-2，则D（1，-2），
过点D作DG⊥CE于点G，
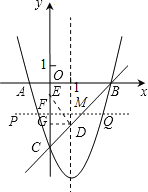
∴DG=1，CG=1，
∴GE=CE-CG=
-1=．
在Rt△EGD中，tan∠CED=
．
②P1（1-，-2），P2（1-，-）．
设OE=a，则GE=2-a，
当CE为斜边时，则DG2=CGGE，即1=（OC-OG）（2-a），
∴1=1×（2-a），
∴a=1，
∴CE=2，
∴OF=OE+EF=2
∴F、P的纵坐标为-2，
把y=-2，代入抛物线的函数表达式为y=x2-2x-3得：x=1+或1-
∵点P在第三象限．
∴P1（1-，-2），
当CD为斜边时，DE⊥CE，
∴OE=2，CE=1，
∴OF=2.5，
∴P和F的纵坐标为：-，
把y=-，代入抛物线的函数表达式为y=x2-2x-3得：x=1-，或1+，
∵点P在第三象限．
∴P2（1-，-）．
综上所述：满足条件为P1（1-，-2），P2（1-，-）．
