题目内容
【题目】已知矩形![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 点出发,以2cm/s的速度沿
点出发,以2cm/s的速度沿![]() 向终点
向终点![]() 匀速运动,连接
匀速运动,连接![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() s .
s .
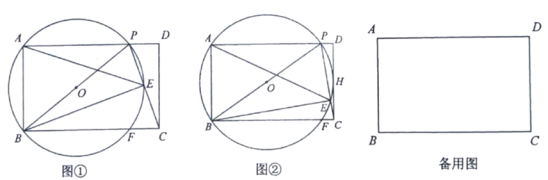
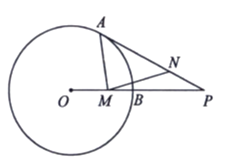
(1)如图①,若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
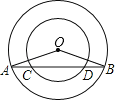
(2)如图②,若⊙![]() 与
与![]() 相切于点
相切于点![]() ,求
,求![]() 的值;
的值;
(3)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() ;(3)2.5或4.
;(3)2.5或4.
【解析】
(1)由已知证明![]() ,推出BC=BP;(2)连接OH,过点O作OM⊥AD于M.由四边形ABCD是矩形,可证
,推出BC=BP;(2)连接OH,过点O作OM⊥AD于M.由四边形ABCD是矩形,可证![]() °,可得OM∥AB,可证
°,可得OM∥AB,可证![]() 可得
可得![]() ,OM=
,OM=![]() AB=3;由AP=2t,可得MP=AM=2t,MD=10-t,可证四边形OMDH是矩形,可得OH=OP=MD=10-t,根据勾股定理可知:在
AB=3;由AP=2t,可得MP=AM=2t,MD=10-t,可证四边形OMDH是矩形,可得OH=OP=MD=10-t,根据勾股定理可知:在![]() 中,
中,![]() ,即可求出t的值;(3)分两种情况讨论,当AE=BE时,则
,即可求出t的值;(3)分两种情况讨论,当AE=BE时,则![]() 由四边形PABE内接于⊙
由四边形PABE内接于⊙![]() ,可得
,可得![]() ,
,
可推![]() ,故PB=BC=10,根据勾股定理在
,故PB=BC=10,根据勾股定理在![]() 中,AP=
中,AP=![]() ,可得2t=8,t=4;若AB=AE,可证
,可得2t=8,t=4;若AB=AE,可证![]() 可得AP=PD=5,
可得AP=PD=5,
即2t=5,解得t=2.5;
(1)证明:∵BP为⊙![]() 直径,
直径,
∴![]() °;
°;
∵点E为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
在![]()
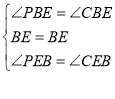
∴![]() ,
,
∴BC=BP;
(2)连接OH,过点O作OM⊥AD于M.
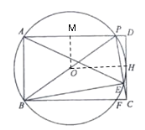
∵四边形ABCD是矩形,
∴![]() °;
°;
∵OM⊥AD,AB⊥AD,
∴OM∥AB;
∴![]() ,
,![]() ,
,
∴OM=![]() AB=3;
AB=3;
∵AP=2t,
∴MP=AM=2t,MD=10-t,
∵⊙![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() °,
°,
∴四边形OMDH是矩形,
∴OH=OP=MD=10-t,
在![]() 中,
中,![]() ,
,
解得t=![]() ;
;
(3)若AE=BE,则![]()
∵四边形PABE内接于⊙![]() ,
,
∴![]() ,
,
∵AD∥BC,
∴![]() ,
,
∴![]() ,
,
∴PB=BC=10,
在![]() 中,AP=
中,AP=![]() ,
,
∴2t=8,t=4;
若AB=AE,
则![]() ,
,
同理可得![]() ,
,
∴![]() ;
;
∵四边形ABCD是矩形,
∴AB=CD;
在![]()
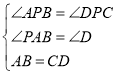
∴![]()
∴AP=PD=5,
即2t=5,解得t=2.5;
综上所述,t的值为2.5或4.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目