题目内容
【题目】求二次函数![]() 的图象如图所示,其对称轴为直线
的图象如图所示,其对称轴为直线![]() ,与
,与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,其中
,其中![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中,正确的结论有( )
;其中,正确的结论有( )
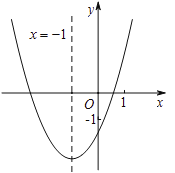
A.5B.4C.3D.2
【答案】C
【解析】
由抛物线开口方向得a>0,由抛物线的对称轴为直线![]() 得
得![]() >0,由抛物线与y轴的交点位置得c<0,则abc<0;由于抛物线与x轴一个交点在点(0,0)与点(1,0)之间,根据抛物线的对称轴性得到抛物线与x轴另一个交点在点(-3,0)与点(-2,0)之间,即有-3<
>0,由抛物线与y轴的交点位置得c<0,则abc<0;由于抛物线与x轴一个交点在点(0,0)与点(1,0)之间,根据抛物线的对称轴性得到抛物线与x轴另一个交点在点(-3,0)与点(-2,0)之间,即有-3<![]() <-2;抛物线的对称轴为直线
<-2;抛物线的对称轴为直线![]() ,且c<-1,
,且c<-1,![]() 时,
时,![]() ;抛物线开口向上,对称轴为直线
;抛物线开口向上,对称轴为直线![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 得:
得:![]() ,且
,且![]() ,∴
,∴![]() ,即
,即![]()
![]() ;对称轴为直线
;对称轴为直线![]() 得
得![]() ,由于
,由于![]() 时,
时,![]() ,则
,则![]() 0,所以
0,所以![]() 0,解得
0,解得![]() ,然后利用
,然后利用![]() 得到
得到![]() .
.
∵抛物线开口向上,∴a>0,
∵抛物线的对称轴为直线![]() ,∴b=2a>0,
,∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc<0,
所以①错误;
∵抛物线![]() 与x轴一个交点在点(0,0)与点(1,0)之间,而对称轴为
与x轴一个交点在点(0,0)与点(1,0)之间,而对称轴为![]() ,由于抛物线与x轴一个交点在点(0,0)与点(1,0)之间,根据抛物线的对称轴性,∴抛物线与x轴另一个交点在点(-3,0)与点(-2,0)之间,即有-3<
,由于抛物线与x轴一个交点在点(0,0)与点(1,0)之间,根据抛物线的对称轴性,∴抛物线与x轴另一个交点在点(-3,0)与点(-2,0)之间,即有-3<![]() <-2,所以②正确;
<-2,所以②正确;
∵抛物线的对称轴为直线![]() ,且c<-1,∴当
,且c<-1,∴当![]() 时,
时,![]() , 所以③正确;
, 所以③正确;
∵抛物线开口向上,对称轴为直线![]() ,∴当
,∴当![]() 时,
时,![]() ,
,
当![]() 代入
代入![]() 得:
得:![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]()
![]() ,所以④错误;
,所以④错误;
∵对称轴为直线![]() ,∴
,∴![]() ,
,
∵由于![]() 时,
时,![]() ,∴
,∴![]() 0,所以
0,所以![]() 0,解得
0,解得![]() ,
,
根据图象得![]() ,∴
,∴![]() ,所以⑤正确.
,所以⑤正确.
所以②③⑤正确, 故选:C.

练习册系列答案
相关题目