题目内容
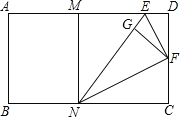
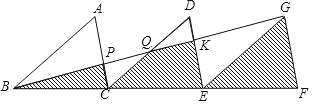
【题目】如图,已知△ABC≌△DCE≌△GEF,三条对应边BC.CE、EF在同一条直线上,连接BG,分别交AC、DC、DE于点P、Q、K,其中S△PQC=3,则图中三个阴影部分的面积和为__.
【答案】39
【解析】
根据全等三角形对应角相等,证明AC∥DE∥HF,再利用对应边相等得BC=CE=EF,根据平行线分线段成比例定理得KE=2PC,HF=3PC,设DK为x,DK边上的高为h,根据S△PQC=3,求出xh=6,再分别表示出S△BPC,S四边形CEKQ,S△EFH的面积进行求和即可.
解:∵△ABC≌△DCE≌△GEF,
∴∠ACB=∠DEC=∠HFE,BC=CE=EF,
∴AC∥DE∥HF,
∴![]() ,
,![]() ,
,
∴KE=2PC,HF=3PC,
又∵DK=DE-KE=3PC-2PC=PC,
∴△DQK≌△CQP(相似比为1)
设△DQK的边DK为x,DK边上的高为h,
则![]() ,整理得xh=6,
,整理得xh=6,
S△BPC=![]() ,
,
S四边形CEKQ=![]()
S△EFH=![]() ,
,
∴图中三个阴影部分的面积和=39.

练习册系列答案
相关题目