题目内容
【题目】中考前，某校文具店以每套5元购进若干套考试用具，为让利考生，该店决定售价不超过7元，在几天的销售中发现每天的销售数量y（套）和售价x（元）之间存在一次函数关系，绘制图象如图．
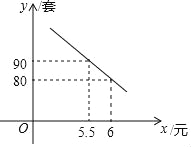
（1）y与x的函数关系式为 （并写出x的取值范围）；
（2）若该文具店每天要获得利润80元，则该套文具的售价为多少元？
（3）设销售该套文具每天获利w元，则销售单价应为多少元时，才能使文具店每天的获利最大？最大利润是多少？
【答案】（1）y=﹣20x+200；（2）6；（3）销售单价应为7元时，才能使文具店每天的获利最大，最大利润是120元．
【解析】
（1）设y与x的函数关系式为：y＝kx+b，把（5.5，90）和（6，80）代入y＝kx+b即可得到结论；
（2）根据题意得方程即可得到结论；
（3）根据题意得二次函数解析式，根据二次函数的性质即可得到结论．
解：（1）设y与x的函数关系式为：y=kx+b，把（5.5，90）和（6，80）代入y=kx+b得： 
解得：
∴y与x的函数关系式为：y=﹣20x+200（5≤x≤7）．
故答案为：y=﹣20x+200；
（2）根据题意得：（x﹣5）（﹣20x+200）=80，解得：x1=6，x2=9（不合题意舍去）．
答：该套文具的售价为6元；
（3）根据题意得：w=（x﹣5）（﹣20x+200）=﹣20x2+300x﹣1000，当
∵7.5＞7，
∴当x=7时，文具店每天的获利最大，最大利润是（7﹣5）（﹣20×7+200）=120（元）．
答：销售单价应为7元时，才能使文具店每天的获利最大，最大利润是120元．
练习册系列答案
通城学典默写能手系列答案
相关题目
