题目内容
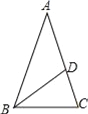
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.
【答案】(1)AD2=ACCD.(2)36°.
【解析】试题分析:(1)通过计算得到![]() =
=![]() ,再计算AC·CD,比较即可得到结论;
,再计算AC·CD,比较即可得到结论;
(2)由![]() ,得到
,得到![]() ,即
,即![]() ,从而得到△ABC∽△BDC,故有
,从而得到△ABC∽△BDC,故有![]() ,从而得到BD=BC=AD,故∠A=∠ABD,∠ABC=∠C=∠BDC.
,从而得到BD=BC=AD,故∠A=∠ABD,∠ABC=∠C=∠BDC.
设∠A=∠ABD=x,则∠BDC=2x,∠ABC=∠C=∠BDC=2x,由三角形内角和等于180°,解得:x=36°,从而得到结论.
试题解析:(1)∵AD=BC=![]() ,∴
,∴![]() =
=![]() =
=![]() .
.
∵AC=1,∴CD=![]() =
=![]() ,∴
,∴![]() ;
;
(2)∵![]() ,∴
,∴![]() ,即
,即![]() ,又∵∠C=∠C,∴△ABC∽△BDC,∴
,又∵∠C=∠C,∴△ABC∽△BDC,∴![]() ,又∵AB=AC,∴BD=BC=AD,∴∠A=∠ABD,∠ABC=∠C=∠BDC.
,又∵AB=AC,∴BD=BC=AD,∴∠A=∠ABD,∠ABC=∠C=∠BDC.
设∠A=∠ABD=x,则∠BDC=∠A+∠ABD=2x,∴∠ABC=∠C=∠BDC=2x,∴∠A+∠ABC+∠C=x+2x+2x=180°,解得:x=36°,∴∠ABD=36°.

练习册系列答案
相关题目
