题目内容
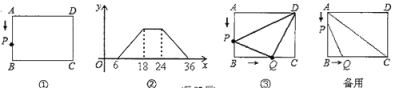
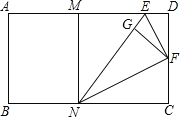
【题目】如图,矩形ABCD,![]() ,
,![]() ,点M,N分别为边AD和边BC上的两点,且
,点M,N分别为边AD和边BC上的两点,且![]() ,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将
,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将![]() 沿着EF所在的直线折叠,将
沿着EF所在的直线折叠,将![]() 沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点
沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点![]() 以下结论中:
以下结论中:
![]() ;
;![]() ;
;![]() ∽
∽![]() ;
;![]() 四边形MNCD是正方形;
四边形MNCD是正方形;![]() 其中正确的结论是
其中正确的结论是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由折叠的性质得到∠DFE=∠GFE,∠GFN=∠CFN,根据平角的定义得到EF⊥NF;故①正确;连接AN,根据轴对称的性质得到∠ANM=∠ENM,推出∠MNE≠∠CNE;故②错误;根据余角的性质得到∠DFE≠∠NEM,推出△MNE∽△DEF错误,故③错误;设DE=x,根据相似三角形的性质得到CN=8,推出四边形MNCD是正方形;故④正确;根据线段的和差得到AM=6,故⑤错误.
∵由折叠的性质得,∠DFE=∠GFE,∠GFN=∠CFN,
∵∠DFE+∠GFE+∠GFN+∠CFN=180°,
∴∠GFN+∠CFN=90°,
∴∠NFE=90°,
∴EF⊥NF;故①正确;
连接AN,
∵点E是点A关于MN所在的直线的对称点,
∴∠ANM=∠ENM,
∴∠ANB=∠CNE,
而四边形ABNM不是正方形,
∴∠ANB≠∠ANM,
∴∠MNE≠∠CNE;故②错误;
∵∠NEF≠90°,∠DFE+∠DEF=90°,∠DEF+∠MEN≠90°,
∴∠DFE≠∠NEM,
∴△MNE∽△DEF错误,故③错误;
设DE=x,
∴BN=AM=![]() ,
,
∴CN=14﹣BN=![]() ,
,
∵∠EFD+∠CFN=∠EFD+∠DEF=90°,
∴∠DEF=∠CFN,
∵∠D=∠C=90°,
∴△DEF∽△CFN,
∴![]() ,
,
∵F是CD的在中点,
∴CF=DF=4,
∴![]() ,
,
∴x=2,x=﹣16(不合题意舍去),
∴DE=2,CN=8,
∴CD=CN,
∴四边形MNCD是正方形;故④正确;
∵CN=DM=8,
∴AM=6,故⑤错误,
故选:B.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案