题目内容
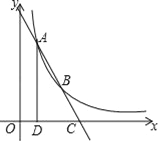
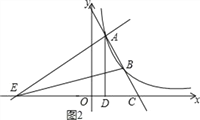
【题目】如图,点A(1,4)、B(2,a)在函数y=![]() (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
【答案】(1)4;(2)C的坐标为(3,0);(3)(﹣2,0).
【解析】试题分析:(1)把点代入求值.(2)先利用反比例函数求出A,B,点坐标,再利用待定系数法求直线方程.(3)假设存在E点,因为![]() ACD是直角三角形,假设
ACD是直角三角形,假设![]() ABE也是直角三角形,利用勾股定理分别计算A,B,C,是直角时AB长度,均与已知矛盾,所以不存在.
ABE也是直角三角形,利用勾股定理分别计算A,B,C,是直角时AB长度,均与已知矛盾,所以不存在.
试题解析:
解:(1)∵点A(1,4)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1×4=4,
故答案为:4.
(2)∵点B(2,a)在反比例函数y=![]() 的图象上,
的图象上,
∴a==2,
∴B(2,2).
设过点A、B的直线的解析式为y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴过点A、B的直线的解析式为y=﹣2x+6.
当y=0时,有﹣2x+6=0,
解得:x=3,
∴点C的坐标为(3,0).
(3)假设存在,设点E的坐标为(n,0).
①当∠ABE=90°时(如图1所示),
∵A(1,4),B(2,2),C(3,0),
∴B是AC的中点,
∴EB垂直平分AC,EA=EC=n+3.
由勾股定理得:AD2+DE2=AE2,即42+(x+1)2=(x+3)2,
解得:x=﹣2,
此时点E的坐标为(﹣2,0);
②当∠BAE=90°时,∠ABE>∠ACD,
故△EBA与△ACD不可能相似;
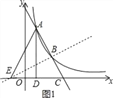
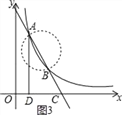
③当∠AEB=90°时,∵A(1,4),B(2,2),
∴AB=![]() ,2>
,2>![]() ,
,
∴以AB为直径作圆与x轴无交点(如图3),
∴不存在∠AEB=90°.
综上可知:在x轴上存在点E,使以A、B、E为顶点的三角形与△ACD相似,点E的坐标为(﹣2,0).

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案