ЬтФПФкШн
ЁОЬтФПЁПзлКЯгыЬНОП
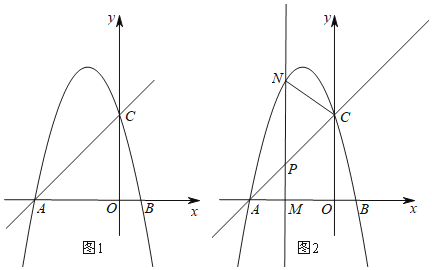
ШчЭМ1ЫљЪОЃЌжБЯпy=x+cгыxжсНЛгкЕуA(-4,0)ЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпy=-x2+bx+cОЙ§ЕуAЃЌCЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪН
(2)ЕуEдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧѓCE+OEЕФзюаЁжЕЃЛ
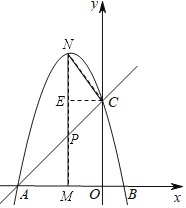
(3)ШчЭМ2ЫљЪОЃЌMЪЧЯпЖЮOAЕФЩЯвЛИіЖЏЕуЃЌЙ§ЕуMДЙжБгкxжсЕФжБЯпгыжБЯпACКЭХзЮяЯпЗжБ№НЛгкЕуPЁЂNЃЎ
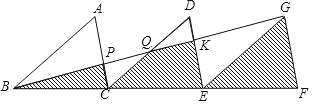
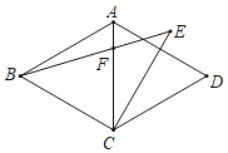
ЂйШєвдCЃЌPЃЌNЮЊЖЅЕуЕФШ§НЧаЮгыЁїAPMЯрЫЦЃЌдђЁїCPNЕФУцЛ§ЮЊЁЁЁЁЃЛ
ЂкШєЕуPЧЁКУЪЧЯпЖЮMNЕФжаЕуЃЌЕуFЪЧжБЯпACЩЯвЛИіЖЏЕуЃЌдкзјБъЦНУцФкЪЧЗёДцдкЕуDЃЌЪЙвдЕуDЃЌFЃЌPЃЌMЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
зЂЃКЖўДЮКЏЪ§y=ax2+bx+c(aЁй0)ЕФЖЅЕузјБъЮЊ(![]() )
)
ЁОД№АИЁП(1)y=-x2-3x+4ЃЛ(2)5ЃЛ(3)Ђй![]() Лђ4ЃЛЂкДцдкЃЌDЕузјБъЮЊ(
Лђ4ЃЛЂкДцдкЃЌDЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )Лђ(-1+
)Лђ(-1+![]() ЃЌ
ЃЌ![]() )Лђ(-1-
)Лђ(-1-![]() ЃЌ-
ЃЌ-![]() )Лђ(-4ЃЌ3).
)Лђ(-4ЃЌ3).
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЬѕМўЧѓГіC,дйНЋЕуAДњШыМДПЩЧѓГіНтЮіЪН.
(2) зіЕу![]() ЙигкХзЮяЯпЕФЖдГЦжсжБЯп
ЙигкХзЮяЯпЕФЖдГЦжсжБЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌСЌ
ЃЌСЌ![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎСЌ
ЃЎСЌ![]() ЃЌИљОнЙДЙЩЖЈРэМДПЩНтД№.
ЃЌИљОнЙДЙЩЖЈРэМДПЩНтД№.
(3)ЂйЗжРрЬжТлВЛЭЌЯрЫЦЧщПіЃЌРћгУЬѕМўЧѓГіЯпЖЮГЄЖШМДПЩНтД№.
ЂкЩш![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЕУГіPЕузјБъЃЌДњШыЪНзгЧѓГіaЃЌИљОнСтаЮаджЪМДПЩЧѓГіDЕузјБъ.
ЃЌЕУГіPЕузјБъЃЌДњШыЪНзгЧѓГіaЃЌИљОнСтаЮаджЪМДПЩЧѓГіDЕузјБъ.
(1)НЋ![]() ДњШы
ДњШы![]()
![]()
НЋ![]() КЭ
КЭ![]() ДњШы
ДњШы![]()
![]()
![]() ХзЮяЯпНтЮіЪНЮЊ
ХзЮяЯпНтЮіЪНЮЊ![]()
(2)зіЕу![]() ЙигкХзЮяЯпЕФЖдГЦжсжБЯп
ЙигкХзЮяЯпЕФЖдГЦжсжБЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌСЌ
ЃЌСЌ![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
СЌ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЕФжЕзюаЁЃЎ
ЕФжЕзюаЁЃЎ
![]() ХзЮяЯпЖдГЦжсЮЛжУЯп
ХзЮяЯпЖдГЦжсЮЛжУЯп![]()
![]()
гЩЙДЙЩЖЈРэ![]()
![]() ЕФзюаЁжЕЮЊ5
ЕФзюаЁжЕЮЊ5
(3)ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
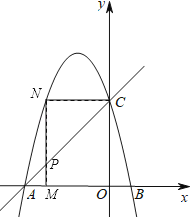
![]() ЃЌдђ
ЃЌдђ![]() ЙигкХзЮяЯпЖдГЦжсЖдГЦ
ЙигкХзЮяЯпЖдГЦжсЖдГЦ
![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]()
ЕБ![]() ЪБ
ЪБ
гЩвбжЊ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]()
Й§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() зјБъЮЊ
зјБъЮЊ![]()
![]() ЃЌ
ЃЌ
дђ![]() ЮЊ
ЮЊ![]() ЃЌ
ЃЌ![]()
![]()
ДњШы![]()
НтЕУ![]()
![]() ЕФУцЛ§ЮЊ4
ЕФУцЛ§ЮЊ4
ЙЪД№АИЮЊЃК![]() Лђ4
Лђ4
ЂкДцдк
Щш![]() зјБъЮЊ
зјБъЮЊ![]()
дђ![]() ЮЊ
ЮЊ![]()
дђ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]()
АбЕу![]() зјБъДњШы
зјБъДњШы![]()
НтЕУ![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ![]()
ЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дк
дк![]() ДЙжБЦНЗжЯпЩЯЃЌдђ
ДЙжБЦНЗжЯпЩЯЃЌдђ![]()
ЕБ![]() ЪБЃЌгЩСтаЮаджЪЕу
ЪБЃЌгЩСтаЮаджЪЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЁЂ
ЁЂ![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЃЌЕу
ЖдГЦЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]()