题目内容
将矩形ABCD沿着直线BD折叠，使点C落在C’处，B C′交AD于E，AD=8，AB=4
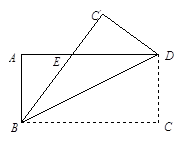
①证明△BED为等腰三角形(4分)
②求△BED的面积(4分)
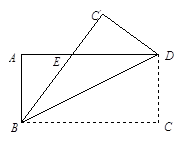
①证明△BED为等腰三角形(4分)
②求△BED的面积(4分)
①证明见解析②10
①证∠EBD＝∠EDB（利用折叠与平等）（4分）
②S△BED＝10（求出DE＝5 S△BED＝
×DE×AB）（4分）
（1）要证△BED是等腰三角形，只需证明∠1=∠2即可，根据翻折的性质∠2=∠3，又∠1=∠3，继而得证；
（2）只需求出ED的长即可求出△BED的面积，设ED=x，则AE=8-x，BE=x，在Rt△ABE中，根据勾股定理即可求出ED的长．
②S△BED＝10（求出DE＝5 S△BED＝
×DE×AB）（4分）（1）要证△BED是等腰三角形，只需证明∠1=∠2即可，根据翻折的性质∠2=∠3，又∠1=∠3，继而得证；
（2）只需求出ED的长即可求出△BED的面积，设ED=x，则AE=8-x，BE=x，在Rt△ABE中，根据勾股定理即可求出ED的长．
练习册系列答案
相关题目
中，点
、
分别在
和
上，
．
；
交
于点
，延长
至点
，使
，连接
、
，判断四边形
是什么特殊四边形？并证明你的结论．
ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗？请说明理由.
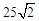
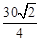
cm，宽为
cm的矩形板材（如图），另一种是边长为
cm的正方形地砖（如图②）
，
=90°．
中，对角线
，那么依次连结四边形
．菱形； 
．矩形； 
．正方形； 
．平行四边形．