题目内容
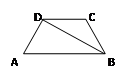
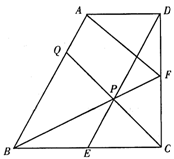
如图,在 ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗?请说明理由.
ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗?请说明理由.
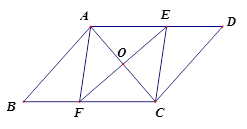
 ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗?请说明理由.
ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗?请说明理由.
解:是菱形 ,理由如下:
 四边形ABCD为平行四边形;
四边形ABCD为平行四边形;
 AD∥BC
AD∥BC
 ∠EAO =∠FCO
∠EAO =∠FCO
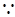 EF⊥AC于O
EF⊥AC于O
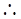 ∠AOE =∠COF
∠AOE =∠COF
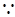 AO=CO
AO=CO
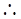 △AOE ≌ △COF (ASA)
△AOE ≌ △COF (ASA)
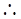 EO=FO
EO=FO
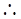 四边形AFCE为菱形(对角线互相垂直且平分的四边形为菱形).
四边形AFCE为菱形(对角线互相垂直且平分的四边形为菱形).
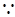 四边形ABCD为平行四边形;
四边形ABCD为平行四边形;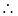 AD∥BC
AD∥BC ∠EAO =∠FCO
∠EAO =∠FCO EF⊥AC于O
EF⊥AC于O ∠AOE =∠COF
∠AOE =∠COF AO=CO
AO=CO △AOE ≌ △COF (ASA)
△AOE ≌ △COF (ASA) EO=FO
EO=FO 四边形AFCE为菱形(对角线互相垂直且平分的四边形为菱形).
四边形AFCE为菱形(对角线互相垂直且平分的四边形为菱形).根据平行四边形性质推出AD∥BC,根据平行线的性质可得∠EAO =∠FCO,再有对顶角∠AOE =∠COF,AO=CO根据“AAS”推出△AOE≌△COF,即有EO=FO,加上AO=CO,可先判断四边形AFCE是平行四边形,再有EF⊥AC,则四边形AFCE是菱形.

练习册系列答案
相关题目
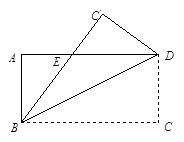

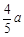
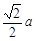
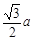
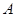 →
→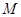 →
→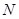 →
→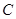 的小路(
的小路( 、
、 中点).极少数同学为了走“捷径”,沿线段
中点).极少数同学为了走“捷径”,沿线段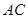 行走,破坏了草坪,实际上他们仅少走了________米。
行走,破坏了草坪,实际上他们仅少走了________米。
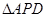 全等的三角形,并说明理由;
全等的三角形,并说明理由;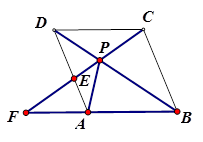
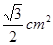
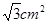
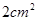
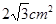
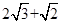 和
和 ,求该矩形的面积和对角线的长.
,求该矩形的面积和对角线的长.