题目内容
已知:如图,在正方形 中,点
中,点 、
、 分别在
分别在 和
和 上,
上, .
.

(1)求证: ;
;
(2)连接 交
交 于点
于点 ,延长
,延长 至点
至点 ,使
,使 ,连接
,连接 、
、 ,判断四边形
,判断四边形 是什么特殊四边形?并证明你的结论.
是什么特殊四边形?并证明你的结论.
 中,点
中,点 、
、 分别在
分别在 和
和 上,
上, .
.
(1)求证:
 ;
;(2)连接
 交
交 于点
于点 ,延长
,延长 至点
至点 ,使
,使 ,连接
,连接 、
、 ,判断四边形
,判断四边形 是什么特殊四边形?并证明你的结论.
是什么特殊四边形?并证明你的结论.(1)证明见解析(2)菱形,证明见解析
(1)证明:∵四边形 是正方形,∴
是正方形,∴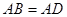 ,
,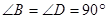 .
.
∵ ,∴Rt
,∴Rt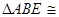 Rt
Rt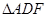 .∴
.∴ .………………………(5分)
.………………………(5分)
(2)四边形 是菱形.…………………………………………………………(7分)
是菱形.…………………………………………………………(7分)
∵四边形 是正方形,∴
是正方形,∴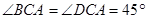 ,
,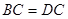 .
.
∵ ,∴
,∴ ,即
,即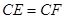 .∴
.∴ ………(10分)
………(10分)
∵ ,∴四边形
,∴四边形 是平行四边形.………………………………(11分)
是平行四边形.………………………………(11分)
∵ ,∴平行四边形
,∴平行四边形 是菱形.……………………………………(12分)
是菱形.……………………………………(12分)
(1)求简单的线段相等,可证线段所在的三角形全等,即证△ABE≌△ADF;
(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相垂直平分,根据对角线互相垂直且平分的四边形是菱形,即可判定四边形AEMF是菱形.
 是正方形,∴
是正方形,∴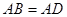 ,
,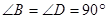 .
.∵
 ,∴Rt
,∴Rt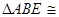 Rt
Rt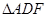 .∴
.∴ .………………………(5分)
.………………………(5分)(2)四边形
 是菱形.…………………………………………………………(7分)
是菱形.…………………………………………………………(7分)∵四边形
 是正方形,∴
是正方形,∴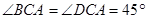 ,
,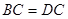 .
.∵
 ,∴
,∴ ,即
,即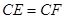 .∴
.∴ ………(10分)
………(10分)∵
 ,∴四边形
,∴四边形 是平行四边形.………………………………(11分)
是平行四边形.………………………………(11分)∵
 ,∴平行四边形
,∴平行四边形 是菱形.……………………………………(12分)
是菱形.……………………………………(12分)(1)求简单的线段相等,可证线段所在的三角形全等,即证△ABE≌△ADF;
(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相垂直平分,根据对角线互相垂直且平分的四边形是菱形,即可判定四边形AEMF是菱形.

练习册系列答案
相关题目
 、
、 是□
是□ 的对角线
的对角线 上的两点,
上的两点, .
.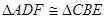 ;(2)
;(2)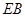 ∥
∥ .
.
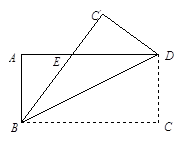

 时,它是菱形
时,它是菱形 时,它是正方形
时,它是正方形 时,它是矩形
时,它是矩形 时,它是菱形
时,它是菱形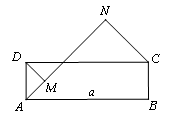




 ,P是线段AC上的一个动点.
,P是线段AC上的一个动点.
 →
→ →
→ →
→ 的小路(
的小路( 、
、 中点).极少数同学为了走“捷径”,沿线段
中点).极少数同学为了走“捷径”,沿线段 行走,破坏了草坪,实际上他们仅少走了________米。
行走,破坏了草坪,实际上他们仅少走了________米。
