题目内容
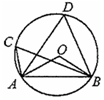
如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连结AB、BC.
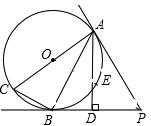
(1)求证△ABC∽△ADB;
(2)若切线AP的长为12厘米,求弦AB的长.

(1)求证△ABC∽△ADB;
(2)若切线AP的长为12厘米,求弦AB的长.
(1)证明:∵AC是圆O的直径,∴∠ABC=90 o,
又∵AD⊥BP,∴∠ADB=90 o,∴∠ABC=∠ADB,
又∵PB是圆的切线,∴∠ABD=∠ACB,
在△ABC和△ADB中:
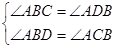 ,∴△ABC∽△ADB;
,∴△ABC∽△ADB;
(2)如图,连结OP,
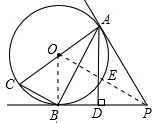
在Rt△AOP中,AP=12厘米,OA=5厘米,根据勾股定理求得OP=13厘米,
又由已知可证得△ABC∽△PAO, ∴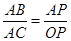 ,得
,得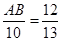 ,解得AB=
,解得AB=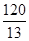 厘米.
厘米.
又∵AD⊥BP,∴∠ADB=90 o,∴∠ABC=∠ADB,
又∵PB是圆的切线,∴∠ABD=∠ACB,
在△ABC和△ADB中:
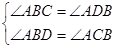 ,∴△ABC∽△ADB;
,∴△ABC∽△ADB;(2)如图,连结OP,

在Rt△AOP中,AP=12厘米,OA=5厘米,根据勾股定理求得OP=13厘米,
又由已知可证得△ABC∽△PAO, ∴
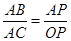 ,得
,得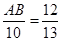 ,解得AB=
,解得AB=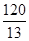 厘米.
厘米.(1)根据AC为⊙O的半径,可知:∠ABC=90°,由AD⊥BP,可知:∠ABC=∠ADB,根据切线的性质知:∠ABD=∠ACB,从而可证:△ABC∽△ADB;
(2)在Rt△POA中,根据勾股定理可将OP的长求出,再根据△ABC∽△PAO,可将AB的长求出.
(2)在Rt△POA中,根据勾股定理可将OP的长求出,再根据△ABC∽△PAO,可将AB的长求出.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
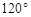 的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm.
的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm. 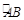 的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4
的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4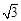 cm.
cm.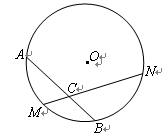
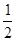 AB,PC切半圆O于点C,点D是
AB,PC切半圆O于点C,点D是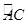 上和点C不重合的一点,则
上和点C不重合的一点,则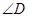 的度数为 .
的度数为 .
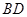 为
为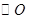 的直径,
的直径,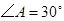 ,则
,则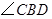 的度数为( )
的度数为( )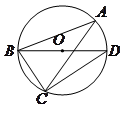
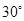
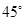
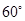
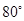
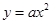 经过C、D两点,则图中阴影部分的面积是 cm2.
经过C、D两点,则图中阴影部分的面积是 cm2.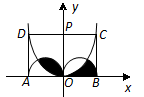
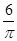 的圆中,60°的圆心角所对的弧长等于 。
的圆中,60°的圆心角所对的弧长等于 。