题目内容
用一张半径为9cm、圆心角为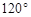 的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm.
的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm.
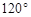 的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm.
的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm. 3
解:半径为9cm、圆心角为120°的扇形弧长是:

设圆锥的底面半径是r,
则2πr=6π,
解得:r=3cm.
这个圆锥形冰淇淋的底面半径是3cm.

设圆锥的底面半径是r,
则2πr=6π,
解得:r=3cm.
这个圆锥形冰淇淋的底面半径是3cm.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目

 、
、 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
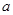 的正
的正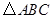 内有一边长为
内有一边长为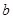 的内接正
的内接正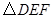 ,则
,则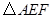 的内切圆半径为 .
的内切圆半径为 .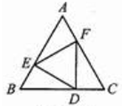

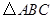 内接于⊙O,
内接于⊙O, 为⊙O的直径,
为⊙O的直径,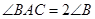 ,
, ,过点
,过点 作⊙O的切线与
作⊙O的切线与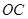 的延长线交于点
的延长线交于点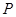 ,求
,求 的长.
的长.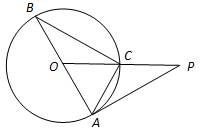
 的外接圆
的外接圆 中,
中, 是
是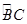 的中点,
的中点,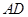 交
交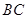 于点
于点 ,连结
,连结 .
. ,若在
,若在 上任取一点
上任取一点 (点
(点 除外),连结
除外),连结 交
交 ,
, 是否成立?若成立,给出证明;若不成立,举例说明.
是否成立?若成立,给出证明;若不成立,举例说明.
