题目内容
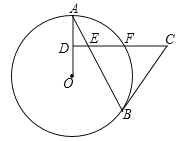
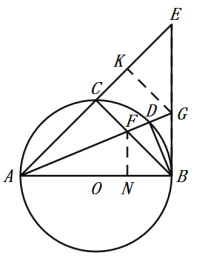
【题目】如图所示,AB是⊙O的直径,点C是弧AB的中点,点D是弧BC的中点,连接AC,BC,AD,BD,且AD与BC相交于点F,延长AC至E,使AC=EC,连接EB交AD的延长线于点G.
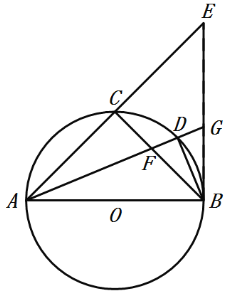
(1)求证:EB是⊙O的切线;
(2)求证;AF=2BD;
(3)求证:线段BG是线段CF和线段EG的比例中项.
【答案】(1)详见解析;(2)详见解析;(3)详见解析
【解析】
(1)由“SAS”可证△ABC≌△EBC,可得∠ABC=∠EBC=45°,可得∠EBA=90°,即可得结论;
(2)延长BD交AE于点M,由“ASA”可证△ADB≌△ADM和△ACF≌△BCM,可得BD=DM,AF=BM=2BD;
(3)过点F作FN⊥AB,过点G作GK⊥AE,由等腰三角形的性质和直角三角形的性质可得BF=![]() CF,EG=
CF,EG=![]() KG=
KG=![]() BG=
BG=![]() BF,即可得结论.
BF,即可得结论.
证明:(1)∵AB是⊙O 的直径,
∴∠ACB=90°
又∵点C是弧AB的中点,
∴∠ABC=45°
又∵AC=EC,∠ACB=∠ECB=90°,BC=BC
∴△ABC≌△EBC(SAS)
∴∠ABC=∠EBC=45°
∴∠EBA=90°,且AB是⊙O 的直径
∴EB是⊙O的切线.
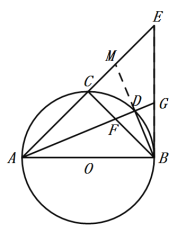
(2)如图,延长BD交AE于点M
∵AB是⊙O 的直径
∴∠ACB=90°,∠ADB=90°
∵点D是弧BC的中点
∴∠MAD=∠BAD=![]() ∠BAC=22.5°,且∠ADB=∠ADM=90°,AD=AD
∠BAC=22.5°,且∠ADB=∠ADM=90°,AD=AD
∴△ADB≌△ADM(ASA)
∴BD=DM
∴BM=2BD
∵点C是弧AB的中点
∴AC=BC,∠ACF=∠BCM=90°,∠CBD=∠CAD
∴△ACF≌△BCM(AAS)
∴AF=BM
∴AF=2BD.
(3)如图,过点F作FN⊥AB,过点G作GK⊥AE,垂足分别为N,K,
由(2)可知∠CAD=∠BAD=22.5°,∠ABC=∠E=45°,
∴∠BFD=∠BAF+∠ABF=22.5°+45°=67.5°,∠BGF=∠CAD+∠E=22.5°+45°=67.5°,
∴∠BFD=∠BGF,
∴BF=BG,
∵∠CAF=∠NAF,FC⊥AE,FN⊥AB,
∴NF=CF,
又∵∠ABC=45°,∠FNB=90°,
∴NF=BN=CF,
∴![]() ,
,
同理![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴BF是线段CF和线段EG的比例中项.
即线段BG是线段CF和线段EG的比例中项.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案