Question

【题目】已知OABC的顶点O与坐标原点重合，点A在x轴正半轴上，点B的坐标为(3，4)，且B，C不在同一象限内，若反比例函数y＝的图象经过线段AB的中点D，则四边形ODBC的面积为____．

Answer 1

【答案】15

【解析】

根据三角形中位线的性质求得点D的纵坐标，代入y=求得点D的坐标，再利用S四边形ODBC=SOABC－S△OAD计算即可．

根据题意，画示意图如解图，分别过点B，D作x轴的垂线，垂足为E，F，

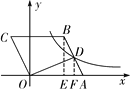
∵B(3，4)，

∴OE=3，BE=4，

∵BE⊥x轴，DF⊥x轴，点D是AB的中点，

∴DF是△ABE的中位线，

∴DF=BE=2，

∵点D在反比例函数y=上，

∴当y=2时，有2=，解得x=4，

∴D(4，2)，即OF=4，

∴EF=4－3=1，

∴AE=2EF=2，

∴OA=5，

∴S四边形ODBC=SOABC－S△OAD

=OA·BE－OA·DF

=5×4－×5×2

=15．