题目内容
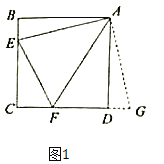
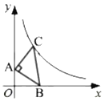
【题目】如图,△ABC与 △ADE中,∠ACB=∠AED=90°,连接BD、CE,∠EAC=∠DAB.
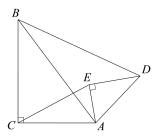
(1)求证:△ABC ∽△ADE;
(2)求证:△BAD ∽△CAE;
(3)已知BC=4,AC=3,AE=![]() .将△AED绕点A旋转,当点E落在线段CD上时,求 BD的长.
.将△AED绕点A旋转,当点E落在线段CD上时,求 BD的长.
【答案】(1)详见解析;(2)详见解析;(3)BD=![]() .
.
【解析】
(1)由已知可得∠CAB=∠EAD,∠ACB=∠AED=90°,则结论得证;
(2)由(1)知![]() ,∠EAC=∠DAB,则结论得证;
,∠EAC=∠DAB,则结论得证;
(3)先证△ABC∽△ADE,求出AE、AD的长,则BD可求.
证明:(1)∵∠EAC=∠DAB,
∴∠CAB=∠EAD,
∵∠ACB=∠AED=90°,
∴△ABC∽△ADE;
(2)由(1)知△ABC∽△ADE,
∴![]() ,
,
∵∠EAC=∠BAD,
∴△BAD∽△CAE;
(3)∵∠ACB=90°,BC=4,AC=3,
∴AB=![]() =5,
=5,
∵△ABC∽△ADE,
∴![]() ,
,
∴AD=![]() ,
,
如图,将△AED绕点A旋转,当点E落在线段CD上时,∠AEC=∠ADB=90°,
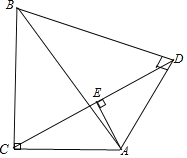
∴BD=![]() .
.

【题目】张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
步行数(步) | 10672 | 4927 | 5543 | 6648 | ||
步行距离(公里) | 6.8 | 3.1 | 3.5 | 4.6 | ||
卡路里消耗(千卡) | 157 | 73 | 82 | 107 | ||
燃烧脂肪(克) | 20 | 10 | 12 | 16 |
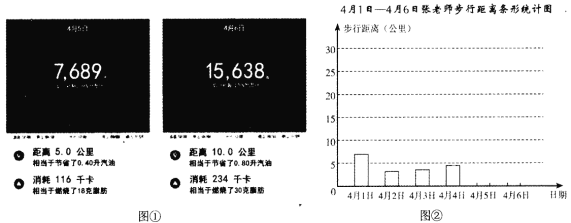
(1).请你将手环记录的4
(2).请你将条形统计图(如图②)补充完整.
(3).张老师这6天平均每天约步行____公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为_____公里(精确到0.1公里).
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.