题目内容
【题目】已知：点E是正方形ABCD中边AB的中点．
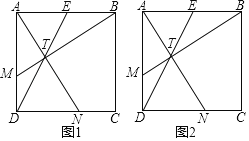
（1）如图1，点T为线段DE上一点，连接BT并延长交AD于点M，连接AT并延长交CD于点N，且AM＝DN．试判断线段AN与线段BM的关系，并证明；求证：点M是线段AD的黄金分割点．
（2）如图2，在AD边上取一点M，满足AM2＝DMDA时，连接BM交DE于点T，连接AT并延长交DC于点N，求tan∠MTD的值．
【答案】（1）AN＝BM，AN⊥BM；证明见解析；（2）
【解析】
（1）AN=BM，AN⊥BM．根据题目给出的条件证明△ABM≌△DAN，从而得出AN=BM，∠ABM=∠DAN，进而得出∠BAN+∠DAN=90°，得出∠ATB=90°，从而得出AN⊥BM；根据题目给出的条件证明△MDT～△TDA，得出DT2=MDAD，再证明DT=AM，即可证明点M是线段AD的黄金分割点；
（2）延长BM，CD交于点F，证明△FMD～△BMA，得出DMAB=AMDF，再根据AB∥CD得出DF=DN=AM，进而证明△ABM≌△DAN，可得∠ATB=90°，证得∠ABM=∠ETB=∠MTD，不妨设正方形的边长为1．设AM=x，由AM2=MDAD，得x2=（1-x）1，求出AM的值，然后根据锐角三角函数的定义解答即可．
解：（1）AN＝BM，AN⊥BM．
理由如下：
∵四边形ABCD是正方形，
∴AB＝DA，∠BAD＝∠ADC＝90°，又AM＝DN，
∴△ABM≌△DAN（SAS），
∴∠ABM＝∠DAN，AN＝BM
又∠BAD＝90°即∠BAN+∠DAN＝90°，
∴∠BAN+∠ABM＝90°
∴∠ATB＝90°，
∴AN⊥BM
∴AN＝BM，AN⊥BM；
证明：∵∠ATB＝90°，M是AB中点．
∴TE＝BE＝AE，
∴∠EBT＝∠ETB，∠EAT＝∠ATE，
又∠ABM＝∠DAN，∠ETB＝∠MTD，
∴∠MTD＝∠DAN，
又∠MDT＝∠ADT，
∴△MDT～△TDA，
∴
，
∴DT2＝MDAD，
由AB∥CD，可得∠TND＝∠EAT，又∠EAT＝∠ATE，∠ATE＝∠DTN，
∴∠TND＝∠DTN
∴DT＝DN，又AM＝DN，
∴DT＝AM，
又DT2＝MDAD，
∴AM2＝MDAD，
∴
，
∴点M是线段AD的黄金分割点；
（2）延长BM，CD交于点F，如图．
∵四边形ABCD是正方形，AB∥CD，
∴∠F＝∠MBA，又∠FMD＝∠AMB，
∴△FMD～△BMA，
∴
，即DMAB＝AMDF，
∵AB＝AD，AM2＝DMAD，
∴AM＝DF，
由AB∥CF知
，
又AE＝BE，
∴DF＝DN＝AM，
由AB＝AD，∠BAM＝∠ADN＝90°，DN＝AM，可证△ABM≌△DAN（SAS），
∴∠ABM＝∠DAN，
∴∠ABT+∠TAB＝∠TAB+∠DAN＝∠span>BAD＝90°，
∴∠ATB＝90°，
又AE＝BE，
∴BE＝ET，
∴∠ABM＝∠ETB＝∠MTD，
设正方形的边长为1．设AM＝x，由AM2＝MDAD，
得x2＝（1﹣x）1，
，
又负值不合题意，舍去．
∴
，
∴
，
在Rt△ABM中，
又∠ABM＝∠MTD，
∴
．
