Question

【题目】如图，是的弦，为半径的中点，过作交弦于点，交于点，且．

（1）求证：是的切线；

（2）连接、，求的度数：

（3）如果，，，求的半径．

Answer 1

【答案】（1）证明见解析； （2）30°；（3）．

【解析】

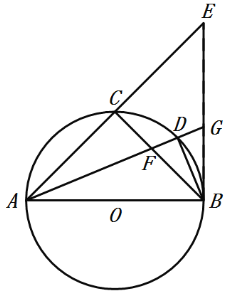
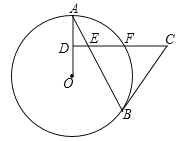
（1）连接OB，由圆的半径相等和已知条件证明∠OBC＝90°，即可证明BC是⊙O的切线；

（2）连接OF，AF，BF，首先证明△OAF是等边三角形，再利用圆周角定理：同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数；

（3）作CG⊥BE于G，如图，利用等腰三角形的性质得BG＝5，再证明∠OAB＝∠ECG，则sin∠ECG＝sin∠OAB＝，于是可计算出CE＝13，从而得到DE＝2，由，得， ，即可求出的半径.

连接．

，，

，，

又．

，

，

，

是的切线；

（2）连接OF，AF，BF，

，，

，

又，

是等边三角形，

，

．

（3）过点作于，

，，

，

∴，

在中，

，sin∠ECG＝sin∠OAB＝，

，，

又，

．

由，得：，

，

的半径为．