ЬтФПФкШн
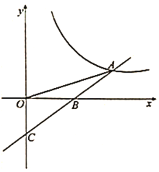
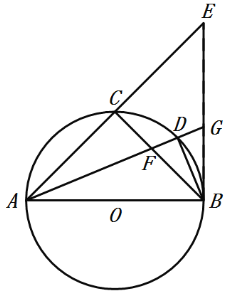
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮOABCЮЊОиаЮЃЌOA=4ЃЌOC=5ЃЌе§БШР§КЏЪ§y=2xЕФЭМЯёНЛABгкЕуDЃЌСЌНгDCЃЌЖЏЕуQДгDЕуГіЗЂбиDCЯђжеЕуCдЫЖЏЃЌЖЏЕуPДгCЕуГіЗЂбиCOЯђжеЕуOдЫЖЏЃЎСНЕуЭЌЪБГіЗЂЃЌЫйЖШОљЮЊУПУы1ИіЕЅЮЛЃЌЩшДгГіЗЂЦ№дЫЖЏСЫt sЃЎ
ЃЈ1ЃЉЧѓЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШєPQЁЮODЃЌЧѓДЫЪБtЕФжЕЃП
ЃЈ3ЃЉЪЧЗёДцдкЪБПЬФГИіtЃЌЪЙSЁїDOP=![]() SЁїPCQЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
SЁїPCQЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЕБtЮЊКЮжЕЪБЃЌЁїDPQЪЧвдDQЮЊбќЕФЕШбќШ§НЧаЮ?
ЁОД№АИЁПЃЈ1ЃЉDЃЈ2ЃЌ4ЃЉЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉДцдкЃЌtЕФжЕЮЊ2 ЃЛЃЈ4ЃЉЕБ
ЃЛЃЈ3ЃЉДцдкЃЌtЕФжЕЮЊ2 ЃЛЃЈ4ЃЉЕБ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЪБЃЌЁїDPQЪЧвЛИівдDQЮЊбќЕФЕШбќШ§НЧаЮ
ЪБЃЌЁїDPQЪЧвЛИівдDQЮЊбќЕФЕШбќШ§НЧаЮ
ЁОНтЮіЁП
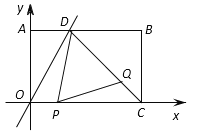
ЃЈ1ЃЉгЩЬтвтЕУГіЕуDЕФзнзјБъЮЊ4ЃЌЧѓГіy=2xжаy=4ЪБxЕФжЕМДПЩЕУЃЛ
ЃЈ2ЃЉгЩPQЁЮODжЄЁїCPQЁзЁїCODЃЌЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌНтжЎПЩЕУЃЛ
ЃЌНтжЎПЩЕУЃЛ
ЃЈ3ЃЉЗжБ№Й§ЕуQЁЂDзїQEЁЭOCЃЌDFЁЭOCНЛOCгыЕуEЁЂFЃЌЖдгкжБЯпy=2xЃЌСюy=4ЧѓГіxЕФжЕЃЌШЗЖЈГіDзјБъЃЌНјЖјЧѓГіBDЃЌBCЕФГЄЃЌРћгУЙДЙЩЖЈРэЧѓГіCDЕФГЄЃЌРћгУСНЖдНЧЯрЕШЕФШ§НЧаЮЯрЫЦЕУЕНШ§НЧаЮCQEгыШ§НЧаЮCDFЯрЫЦЃЌгЩЯрЫЦЕУБШР§БэЪОГіQEЃЌгЩЕзPCЃЌИпQEБэЪОГіШ§НЧаЮPQCУцЛ§ЃЌдйБэЪОГіШ§НЧаЮODPУцЛ§ЃЌвРОнSЁїDOP=![]() SЁїPCQСаГіЙигкtЕФЗНГЬЃЌНтжЎПЩЕУЃЛ
SЁїPCQСаГіЙигкtЕФЗНГЬЃЌНтжЎПЩЕУЃЛ
ЃЈ4ЃЉгЩШ§НЧаЮCQEгыШ§НЧаЮCDFЯрЫЦЃЌРћгУЯрЫЦЕУБШР§БэЪОГіCEЃЌPEЃЌНјЖјРћгУЙДЙЩЖЈРэБэЪОГіPQ2ЃЌDP2ЃЌвдМАDQЃЌЗжСНжжЧщПіПМТЧЃКЂйЕБDQ=DPЃЛЂкЕБDQ=PQЃЌЧѓГіtЕФжЕМДПЩЃЎ
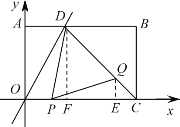
НтЃКЃЈ1ЃЉЁпOA=4
ЁрАб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]()
ЁрDЃЈ2ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉдкОиаЮOABCжаЃЌOA=4ЃЌOC=5
ЁрAB=OC=5ЃЌBC=OA=4
ЁрBD=3ЃЌDC=5
гЩЬтвтжЊЃКDQ=PC=t
ЁрOP=CQ=5t
ЁпPQЁЮOD
Ёр![]()
Ёр![]()
Ёр![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЗжБ№Й§ЕуQЁЂDзїQEЁЭOCЃЌ DFЁЭOCНЛOCгыЕуEЁЂF

дђDF=OA=4
ЁрDFЁЮQE
ЁрЁїCQE ЁзЁїCDF
Ёр![]()
Ёр![]()
Ёр![]()
Ёп SЁїDOP=![]() SЁїPCQ
SЁїPCQ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ![]()
ЕБt=5ЪБЃЌЕуPгыЕуOжиКЯЃЌВЛЙЙГЩШ§НЧаЮЃЌгІЩсШЅ
ЁрtЕФжЕЮЊ2ЃЎ
ЃЈ4ЃЉЁпЁїCQE ЁзЁїCDF
Ёр![]()
Ёр![]()
![]()
Ёр![]()
![]()
![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтжЎЕУЃК![]()
![]()
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
НтжЎЕУЃК![]()
Д№ЃКЕБ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЪБЃЌЁїDPQЪЧвЛИівдDQЮЊбќЕФЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїDPQЪЧвЛИівдDQЮЊбќЕФЕШбќШ§НЧаЮЃЎ