Question

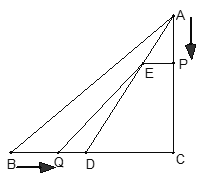
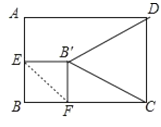
【题目】如图在矩形 ABCD 中 AB=8，BC=6，AE=BE，点 F 为边 BC 上任意一点，将BEF 沿着 EF 翻折，点 B 为点 B 的对应点，则当BCD 的面积最小时BCF 的面积为（ ）

A.4B.6C.4.2D.3

Answer 1

【答案】A

【解析】

当△B′CD面积最小时，B′到CD的距离最小，即B′到AB的距离最大，当B′到AB的距离＝EB′时，此时B′到AB的距离最大，即EB′⊥AB，根据折叠的性质得到BE＝B′E，∠B＝∠EB′F＝∠B′EB＝90，推出四边形EBFB′是正方形，得到B’F=BE=4,FC=BC-BF=2，于是得到BCF 的面积．

当△B′CD面积最小时，B′到CD的距离最小，即B′到AB的距离最大，

∴当B′到AB的距离＝EB′时，此时B′到AB的距离最大，

即EB′⊥AB，

∵将△BEF沿EF翻折，点B的对应点为B′，

∴BE＝B′E，∠B＝∠EB′F＝∠B′EB＝90，

∴四边形EBFB′是正方形，

∴B’F=BE=AB=4=BF,FC=BC-BF=2，

∴当△B′CD面积最小时BCF 的面积=FC×B’F=×2×4=4

故选A．