题目内容
【题目】在
中，
现有两个动点P、Q分别从点A和点B同时出发，其中点P以1cm/s的速度，沿AC向终点C移动；点Q以1.25cm/s的速度沿BC向终点C移动．过点P作PE∥BC交AD于点E，连结EQ．设动点运动时间为x秒．
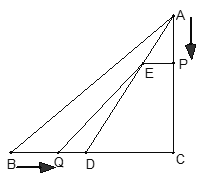
（1）用含x的代数式表示AE、DE的长度；
（2）当点Q在BD（不包括点B、D）上移动时，设
的面积为
，求
与月份
的函数关系式，并写出自变量的取值范围；
（3）当为何值时，为直角三角形．
【答案】详见解析
【解析】
（1）通过△AEP∽△ADC，列出比例关系，即可用含x的代数式表示AE、DE的长度；
（2）Q在BD上运动x秒后，求出DQ、CP，即可表示y与时间x的函数关系式，直接写出自变量x的取值范围；
（3）通过∠EQP=90°，∠QED=90°，分别通过三角形相似，列出比例关系，求出x的值，说明△EDQ为直角三角形．
解：（1）在
，
（2）
，
当点Q在BD上运动x秒后，DQ＝2－1.25x,则
即y与x的函数解析式为：
，其中自变量的取值范围是：0＜x<1.6
(3)分两种情况讨论：
①当
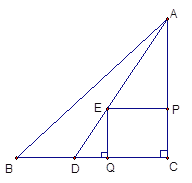
②当
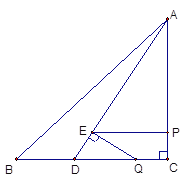
综上所述，当x为2.5秒或3.1秒时，
为直角三角形．
名校课堂系列答案
【题目】距离中考体考时间越来越近，年级想了解初三年级1000名学生周末在家体育锻炼的情况，在初三年级随机抽取了20名男生和20名女生，对他们周末在家的锻炼时间进行了调查，并收集得到了以下数据（单位：min）：
男生：20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生：75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
统计数据，并制作了如下统计表：
时间 x | x≤30 | 30＜x≤60 | 60＜x≤90 | 90＜x≤120 | |
男生 | 2 | 8 | 8 | 2 | |
女生 | 1 | m | n | 3 |
分析数据：两组数据的极差、平均数、中位数、众数如下表所示
极差 | 平均数 | 中位数 | 众数 | |
男生 | a | 65.75 | b | 90 |
女生 | c | 75.5 | 75 | d |
（1）请将上面的表格补充完整：m＝ ，n＝ ，a＝ ，b＝ ，c＝ ，d＝
（2）已知该年级男女生人数差不多，根据调查的数据，估计初三年级周末在家锻炼的时间在 90min 以上的同学约有多少人？
（3）李老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好，请你结合统计数据，写出两条支持李老师观点的理由．
