题目内容
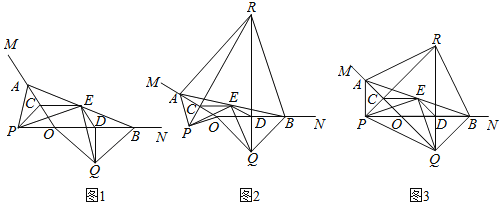
【题目】如图1,A,B分别在射线OM,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.
①如图2,若∠MON=150°,求证:△ABR为等边三角形;
②如图3,若△ARB∽△PEQ,求∠MON大小和![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析,②∠MON=135°,![]() =
=![]() .
.
【解析】
(1)根据三角形中位线的性质得到DE=OC,∥OC,CE=OD,CE∥OD,推出四边形ODEC是平行四边形,于是得到∠OCE=∠ODE,根据等腰直角三角形的定义得到∠PCO=∠QDO=90°,根据等腰直角三角形的性质得到得到PC=ED,CE=DQ,即可得到结论
(2)①连接RO,由于PR与QR分别是OA,OB的垂直平分线,得到AP=OR=RB,由等腰三角形的性质得到∠ARC=∠ORC,∠ORQ=∠BRO,根据四边形的内角和得到∠CRD=30°,即可得到结论;
②由(1)得,EQ=EP,∠DEQ=∠CPE,推出∠PEQ=∠ACR=90°,证得△PEQ是等腰直角三角形,根据相似三角形的性质得到∠ARB=∠PEQ=90°,根据四边形的内角和得到∠MON=135°,求得∠APB=90°,根据等腰直角三角形的性质得到结论.
(1)证明:∵点C、D、E分别是OA,OB,AB的中点,
∴DE=OC,DE∥OC,CE=OD,CE∥OD,
∴四边形ODEC是平行四边形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO+∠EDO=∠EDQ,
∵![]() ,
,![]() ,
,
在△PCE与△EDQ中,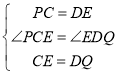 ,
,
∴△PCE≌△EDQ;
(2)①如图2,连接RO,
∵PR与QR分别是OA,OB的垂直平分线,
∴AR=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形;
②由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,∵△ARB∽△PEQ,∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,![]() ,
,
∴∠MON=135°,
此时P,O,B在一条直线上,△PAB为直角三角形,且∠APB=90°,
∴![]() ,∴
,∴![]() .
.
故答案是:(1)见解析;(2)①见解析,②∠MON=135°,![]() .
.

 阅读快车系列答案
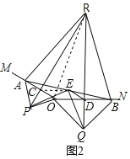
阅读快车系列答案【题目】如图,P是半圆O中![]() 所对弦AB上一动点,过点P作PM⊥AB交
所对弦AB上一动点,过点P作PM⊥AB交![]() 于点M,作射线PN交
于点M,作射线PN交![]() 于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
小超根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4.2 | 2.9 | 2.6 | 2.0 | 1.6 | 0 |
(说明:补全表格时相关数值保留一位小数)
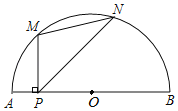
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当MN=2AP时,AP的长度约为 cm.
【题目】如图,抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc<0;②a﹣b+c>0;③2a+b=0;④b2﹣4ac<0;正确的有( )个.
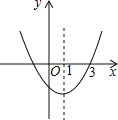
A.1B.2C.3D.4
【题目】距离中考体考时间越来越近,年级想了解初三年级1000名学生周末在家体育锻炼的情况,在初三年级随机抽取了20名男生和20名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:min):
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
统计数据,并制作了如下统计表:
时间 x | x≤30 | 30<x≤60 | 60<x≤90 | 90<x≤120 | |
男生 | 2 | 8 | 8 | 2 | |
女生 | 1 | m | n | 3 |
分析数据:两组数据的极差、平均数、中位数、众数如下表所示
极差 | 平均数 | 中位数 | 众数 | |
男生 | a | 65.75 | b | 90 |
女生 | c | 75.5 | 75 | d |
(1)请将上面的表格补充完整:m= ,n= ,a= ,b= ,c= ,d=
(2)已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在 90min 以上的同学约有多少人?
(3)李老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持李老师观点的理由.