题目内容
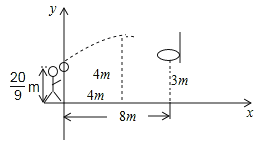
【题目】小明跳起投篮，球出手时离地面
m，球出手后在空中沿抛物线路径运动，并在距出手点水平距离4m处达到最高度4m.已知篮筐中心距地面3m，与球出手时的水平距离为8m，建立如图所示的平面直角坐标系.
（1）求此抛物线对应的函数关系式；
（2）此次投篮，球能否直接命中篮筐中心？若能，请说明理由；若不能，在出手的角度和力度都不变的情况下，球出手时距离地面多少米可使球直接命中篮筐中心？
【答案】（1）y=
；(2）不能正中篮筐中心；3米.
【解析】试题分析：（1）根据顶点坐标（4，4），设抛物线的解析式为：y=
，由球出手时离地面
m，可知抛物线与y轴交点为（0，），代入可求出a的值，写出解析式；
（2）先计算当x=8时，y的值是否等于3，把x=8代入得：y=，所以要想球经过（8，3），则抛物线得向上平移3﹣=
个单位，即球出手时距离地面3米可使球直接命中篮筐中心．
试题解析：（1）设抛物线为y=，
将（0，）代入，得
=，
解得a=
，
∴所求的解析式为y=；
（2）令x=8，得y=
=≠3，
∴抛物线不过点（8，3），
故不能正中篮筐中心；
∵抛物线过点（8，），
∴要使抛物线过点（8，3），可将其向上平移个单位长度，故小明需向上多跳m再投篮（即球出手时距离地面3米）方可使球正中篮筐中心．
练习册系列答案
相关题目
【题目】高速路上因赶时间超速而频频发生交通事故，这样给自己和他人的生命安全带来直接影响，为了解车速情况，一名执法交警在高速路上随机测试了6个小轿车的车速情况记录如下：
车序号 | 1 | 2 | 3 | 4 | 5 | 6 |
车速（千米/时） | 100 | 95 | 106 | 100 | 120 | 100 |
则这6辆车车速的众数和中位数（单位：千米/时）分别是（ ）
A.100，95
B.100，100
C.102，100
D.100，103
