题目内容
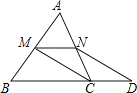
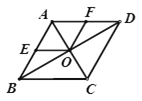
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E、F分别是AB、AD的中点.
(1)若AC=10,BD=24,求菱形ABCD的周长;
(2)连接OE、OF,若AB⊥BC,则四边形AEOF是什么特殊四边形?请说明理由.
【答案】(1)菱形ABCD的周长是52;(2)菱形AEOF是正方形,理由见解析
【解析】分析(1) 根据菱形的性质:对角线互相垂直,利用勾股定理求出AB,即可求解;
(2)首先判断四边形AEOF是平行四边形,再判断平行四边形AEOF是菱形.即可得解.
详解:(1)∵四边形ABCD是菱形,
∴AO=CO,BO=DO,AC⊥BD,
∵AC=10,BD=24,
∴ AO=5,BO=12,
∴AB=13,
∴菱形ABCD的周长是52.
(2)若AB⊥BC,则四边形AEOF是正方形,理由如下:
∵E、O分别是AB、BD中点,∴OE∥AD, 即:OE∥AF,
同理可证:OF∥AE,
∴四边形AEOF是平行四边形,
∵AB=AD,∴AE=AF,
∴平行四边形AEOF是菱形.
∵AB⊥BC,∴∠BAD=90°,
所以菱形AEOF是正方形.
点睛: 此题主要考查了菱形的性质以及三角形中位线定理是解题关键.

练习册系列答案
相关题目