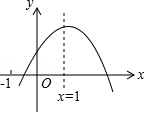��Ŀ����
����Ŀ��ij����������20��������1200̨GH�͵��Ӳ�Ʒ����������֪ÿ̨GH�Ͳ�Ʒ��4��G��װ�ú�3��H��װ��������ɣ���������80�����ˣ�ÿ������ÿ���ܼӹ�6��G��װ�û�3��H��װ�ã����������й��˷ֳ�����ͬʱ��ʼ�ӹ���ÿ��ֱ�ӹ�һ��װ�ã���Ҫ��ÿ��ӹ���G��H��װ����������ȫ���������GH�Ͳ�Ʒ��
��1������������������ʽ������ÿ����������ɶ�����GH�͵��Ӳ�Ʒ�����г���Ԫһ�η�����������⣮
��2��Ϊ���ڹ涨�������������������������һЩ�¹��ˣ���Щ�¹���ֻ�ܶ�������G��װ�õļӹ�����ÿ��ÿ��ֻ�ܼӹ�4��G��װ�ã�1����ԭ��ÿ�찲��x����������G��װ�ã���������m���¹��ˣ���x��ֵ���ú�m�Ĵ���ʽ��ʾ��2������������Ҫ����������¹��˲����ڹ涨�������������
���𰸡���1������ÿ�����������48��GH�͵��Ӳ�Ʒ;��2�� 30����
�������������������1����x�˼ӹ�G��װ�ã�y�˼ӹ�H��װ�ã�����ÿ������ÿ���ܼӹ�6��G��װ�û�3��H��װ�õó���ʽ����𰸣�
��2������ÿ��ӹ���G��H��װ����������ȫ���������GH�Ͳ�Ʒ�ó���ʽ��ʾ��x��ֵ���������ò���ʽ�ⷨ�ó��𰸣�
�����������1���⣺��x�˼ӹ�G��װ�ã�y�˼ӹ�H��װ�ã�������ɵã�
![]()
��ã� ![]() ��
��
6��32��4=48���ף���
�𣺰���������������ʽ������ÿ�����������48��GH�͵��Ӳ�Ʒ��
��2���������֪��3��6x+4m��=3��80-x����4��
��ã�x��![]() ��
��
![]() ��4=240��������
��4=240��������
6x+4m��240
6��![]() +4m��240��
+4m��240��
��ã�m��30��
��������Ҫ����30���¹��˲����ڹ涨�������������