题目内容
【题目】定义一种对正整数n的“C运算”：①当n为奇数时，结果为
；②当n为偶数时，结果为
（其中k是使为奇数的正整数）.“C运算”不停地重复进行，例如，
时，其“C运算”如下：
…若
，则第2020次“C运算”的结果是________.
【答案】1
【解析】
计算出n=35时第一、二、三、四、五、六、七、八次运算的结果，找出规律再进行解答即可．
解：若n=35，第一次结果为35×3+1=106，
第2次结果为：
，
第3次“C运算”的结果是：53×3+1=160
第4次结果为：
，
第5次结果为：5×3+1=16，
第6次结果为：
，
第7次结果为：1×3+1=4，
第8次结果为：
…
可以看出，从第6次开始，结果就只是1，4两个数轮流出现，
且当次数为偶数时，结果是1，次数是奇数时，结果是4，
第2020次是偶数，结果是1，
故答案为：1．
练习册系列答案
每课必练系列答案
相关题目
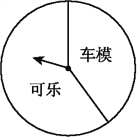
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
