题目内容
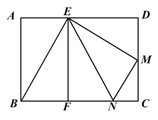
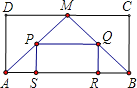
【题目】如图，在矩形ABCD中，M为CD的中点，连接AM、BM，分别取AM、BM的中点P、Q，以P、Q为顶点作第二个矩形PSRQ，使S、R在AB上
在矩形PSRQ中，重复以上的步骤继续画图
若
，矩形ABCD的周长为
则：
______；
第n个矩形的边长分别是______．
【答案】 10 
【解析】分析：
，且M为CD的中点，
，可得
，可得
，再根据矩形ABCD的周长为30，可求的CD的长．
由第一问求得：第一个矩形的长为：10，宽为5，根据三角形中位线定理，
，则宽为
，由此以此类推可得第n个矩形的边长．
详解：
，且M为CD的中点，，
，
又已知矩形ABCD的周长为30，所以
，
故答案为10，
由第一问求得：第一个矩形的长为：10，宽为5，
又点P、Q是AM、BM的中点，所以之后得到的矩形长宽比例为2：1，
在
中，，则宽为，
则可得出：第n个矩形的边长分别是
，
故答案为，
练习册系列答案
阅读快车系列答案
相关题目
