题目内容
【题目】四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF,
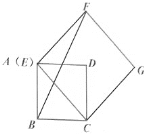
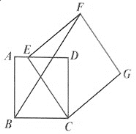
图1 图2
(1)如图1,当点E与点A重合时,则![]() _____;
_____;
(2)如图2,当点E在线段AD上时,![]() ,
,
①求点F到AD的距离;
②求BF的长.
【答案】(1)![]() ;(2)①点F到AD的距离为3;②BF=
;(2)①点F到AD的距离为3;②BF=![]() .
.
【解析】
(1)根据勾股定理依次求出AC、CF、BF长即可;
(2)①过点F作![]() ,由正方形的性质可证
,由正方形的性质可证![]() ,根据全等三角形的性质可得FH的长;②延长FH交BC的延长线于点K,求出BK、FK的长,根据勾股定理可得解.
,根据全等三角形的性质可得FH的长;②延长FH交BC的延长线于点K,求出BK、FK的长,根据勾股定理可得解.
解:(1) 当点E与点A重合时,点C、D、F在一条直线,连接CF,在![]() 中,
中,![]() ,同理可得
,同理可得![]()
![]()

(2)①过点F作![]() 交AD的延长线于点H,如图所示
交AD的延长线于点H,如图所示
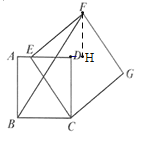
∵四边形CEFG是正方形,
∴![]() ,
,![]()
∴![]() ,
,
又∵四边形ABCD是正方形,
∴![]()
∴![]() ,
,
∴![]()
又∵![]() ,
,
∴![]()
∴![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即点F到AD的距离为3.
,即点F到AD的距离为3.
②延长FH交BC的延长线于点K,如图所示
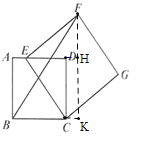
∴![]() ,
,
∴四边形CDHK为矩形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目