题目内容

【题目】已知：如图，在△ABC中，M、N分别是边AB、AC的中点，D是边BC延长线上的一点，且，联结CM、DN．

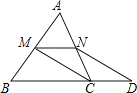
（1）求证：四边形MCDN是平行四边形；

（2）若三角形AMN的面积等于5，求梯形MBDN的面积。

【答案】(1)见解析;(2)20.

【解析】

根据三角形中位线的性质可得MN∥BC，且MN=BC，再由条件CD=BC可得MN=CD，进而可根据一组对边平行且相等的四边形是平行四边形得四边形MCDN是平行四边形．

（1）证明：∵M、N分别是边AB、AC的中点

∴MN∥BC且，

又

∴MN∥CD，且MN=CD

∴四边形MCDN是平行四边形。

（2）∵M、N分别是边AB、AC的中点，四边形MCDN是平行四边形，∴ , , ∴=4×5=20,

∴梯形MBDN的面积等于20.

练习册系列答案
相关题目

【题目】一艘轮船和一艘快艇沿相同的路线从甲港出发驶向乙港的过程中，路程随时间变化的图像如图示（分别是正比例函数的图像和一次函数的图像）.根据图中提供的信息解答下列问题：

（1）分别求出表示轮船和快艇行驶过程中路程和时间之间的函数解析式（不要求写出自变量的取值范围）；

（2）轮船和快艇在途中（不包括起点和终点）行驶的速度分别是多少？

（3）快艇出发多长时间赶上轮船？

【题目】已知：如图，OC是∠AOB的平分线．

（1）当∠AOB = 60°时，求∠AOC的度数；

（2）在（1）的条件下，过点O作OE⊥OC，补全图形，并求∠AOE的度数；

（3）当∠AOB =时，过点O作OE⊥OC，直接写出∠AOE的度数（用含代数式表示）．

【题目】．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（ ）

A. 4个 B. 3个 C. 2个 D. 1个

【题目】〖定义〗:若关于的一元一次方程的解恰好为即，则称该方程为“友好方程”.例如：方程的解为，而，则方程为“友好方程”.

〖运用〗:（1）①，②③三个方程中，为“友好方程”的是______（填写序号）

（2）若关于的一元一次方程是“友好方程”，求的值；

（3）若关于的一元一次方程是“友好方程”，求的值.

【题目】某商店试销一种成本为10元的文具.经试销发现，每天销售件数y（件）是每件销售价格x (元)的一次函数，且当每件按15元的价格销售时，每天能卖出50件；当每件按20元的价格销售时，每天能卖出40件．

（1）试求y关于x的函数解析式（不用写出定义域）；

（2）如果每天要通过销售该种文具获得450元的利润，那么该种文具每件的销售价格应该定为多少元？（不考虑其他因素）

【题目】已知：二次函数y=ax2+2ax﹣4（a≠0）的图象与x轴交于点A，B（A点在B点的左侧），与y轴交于点C，△ABC的面积为12．

（1）求二次函数图象的对称轴与它的解析式；

（2）点D在y轴上，当以A、O、D为顶点的三角形与△BOC相似时，求点D的坐标；

（3）点D的坐标为（﹣2，1），点P在二次函数图象上，∠ADP为锐角，且tan∠ADP=2，求点P的横坐标．

【题目】已知：关于x的一元二次方程：（m﹣1）x2+（m﹣2）x﹣1=0（m为实数）．

（1）若方程有两个不相等的实数根，求m的取值范围；

（2）若是此方程的实数根，抛物线y=（m﹣1）x2+（m﹣2）x﹣1与x轴交于A、B，抛物线的顶点为C，求△ABC的面积．

【题目】如图，菱形ABCD的对角线AC、BD相交于点O，点E、F分别是AB、AD的中点．

（1）若AC＝10，BD＝24，求菱形ABCD的周长；

（2）连接OE、OF，若AB⊥BC，则四边形AEOF是什么特殊四边形？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网