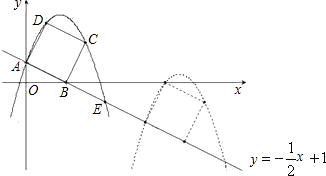
题目内容
如图1,已知:抛物线y=
x2+bx+c与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是y=
x-2,连接AC.
(1)B、C两点坐标分别为B(______,______)、C(______,______),抛物线的函数关系式为______;
(2)判断△ABC的形状,并说明理由;
(3)若△ABC内部能否截出面积最大的矩形DEFC(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.
| 1 |
| 2 |
| 1 |
| 2 |
(1)B、C两点坐标分别为B(______,______)、C(______,______),抛物线的函数关系式为______;
(2)判断△ABC的形状,并说明理由;
(3)若△ABC内部能否截出面积最大的矩形DEFC(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.

(1)令x=0,y=-2,
当y=0代入y=
x-2得出:x=4,
故B,C的坐标分别为:
B(4,0),C(0,-2).(2分)
y=
x2-
x-2.(4分)
(2)△ABC是直角三角形.(5分)
证明:令y=0,则
x2-
x-2=0.
∴x1=-1,x2=4.
∴A(-1,0).(6分)
解法一:∵AB=5,AC=
,BC=2
.(7分)
∴AC2+BC2=5+20=25=AB2.
∴△ABC是直角三角形.(8分)
解法二:∵AO=1,CO=2,BO=4,
∴
=
=
∵∠AOC=∠COB=90°,
∴△AOC∽△COB.(7分)
∴∠ACO=∠CBO.
∵∠CBO+∠BCO=90°,
∴∠ACO+∠BCO=90度.
即∠ACB=90度.
∴△ABC是直角三角形.(8分)
(3)能.①当矩形两个顶点在AB上时,如图1,CO交GF于H.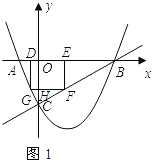
∵GF∥AB,
∴△CGF∽△CAB.
∴
=
.(9分)
解法一:设GF=x,则DE=x,
CH=
x,DG=OH=OC-CH=2-
x.
∴S矩形DEFG=x•(2-
x)=-
x2+2x=-
(x-
)2+
.(10分)
当x=
时,S最大.
∴DE=
,DG=1.
∵△ADG∽△AOC,
∴
=
,
∴AD=
,
∴OD=
,OE=2.
∴D(-
,0),E(2,0).(11分)
解法二:设DG=x,则DE=GF=
.
∴S矩形DEFG=x•
=-
x2+5x=-
(x-1)2+
.(10分)
∴当x=1时,S最大.
∴DG=1,DE=
.
∵△ADG∽△AOC,
∴
=
,
∴AD=
,
∴OD=
,OE=2.
∴D(-
,0),E(2,0).(11分)
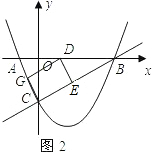
②当矩形一个顶点在AB上时,F与C重合,如图2,
∵DG∥BC,
∴△AGD∽△ACB.
∴
=
.
解法一:设GD=x,
∴AC=
,BC=2
,
∴GF=AC-AG=
-
.
∴S矩形DEFG=x•(
-
)=-
x2+
x
=-
(x-
)2+
.(12分)
当x=
时,S最大.∴GD=
,AG=
,
∴AD=
=
.
∴OD=
∴D(
,0)(13分)
解法二:设DE=x,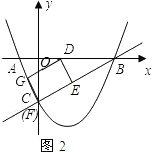
∵AC=
,BC=2
,
∴GC=x,AG=
-x.
∴GD=2
-2x.
∴S矩形DEFG=x•(2
-2x)=-2x2+2
x=-2(x-
)2+
(12分)
∴当x=
时,S最大,
∴GD=
,AG=
.
∴AD=
=
.
∴OD=
∴D(
,0)(13分)
综上所述:当矩形两个顶点在AB上时,坐标分别为(-
,0),(2,0)
当矩形一个顶点在AB上时,坐标为(
,0).(14分)
当y=0代入y=
| 1 |
| 2 |
故B,C的坐标分别为:
B(4,0),C(0,-2).(2分)
y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)△ABC是直角三角形.(5分)
证明:令y=0,则
| 1 |
| 2 |
| 3 |
| 2 |
∴x1=-1,x2=4.
∴A(-1,0).(6分)
解法一:∵AB=5,AC=
| 5 |
| 5 |
∴AC2+BC2=5+20=25=AB2.
∴△ABC是直角三角形.(8分)
解法二:∵AO=1,CO=2,BO=4,
∴
| CO |
| BO |
| AO |
| OC |
| 1 |
| 2 |
∵∠AOC=∠COB=90°,
∴△AOC∽△COB.(7分)
∴∠ACO=∠CBO.
∵∠CBO+∠BCO=90°,
∴∠ACO+∠BCO=90度.
即∠ACB=90度.
∴△ABC是直角三角形.(8分)
(3)能.①当矩形两个顶点在AB上时,如图1,CO交GF于H.

∵GF∥AB,
∴△CGF∽△CAB.
∴
| GF |
| AB |
| CH |
| CO |
解法一:设GF=x,则DE=x,
CH=
| 2 |
| 5 |
| 2 |
| 5 |
∴S矩形DEFG=x•(2-
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 2 |
当x=
| 5 |
| 2 |
∴DE=
| 5 |
| 2 |
∵△ADG∽△AOC,
∴
| AD |
| AO |
| DG |
| OC |
∴AD=
| 1 |
| 2 |
∴OD=
| 1 |
| 2 |
∴D(-
| 1 |
| 2 |
解法二:设DG=x,则DE=GF=
| 10-5x |
| 2 |
∴S矩形DEFG=x•
| 10-5x |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∴当x=1时,S最大.
∴DG=1,DE=
| 5 |
| 2 |
∵△ADG∽△AOC,
∴
| AD |
| AO |
| DG |
| OC |
∴AD=
| 1 |
| 2 |
∴OD=
| 1 |
| 2 |
∴D(-
| 1 |
| 2 |
②当矩形一个顶点在AB上时,F与C重合,如图2,
∵DG∥BC,
∴△AGD∽△ACB.
∴
| GD |
| BC |
| AG |
| AF |

解法一:设GD=x,
∴AC=
| 5 |
| 5 |
∴GF=AC-AG=
| 5 |
| x |
| 2 |
∴S矩形DEFG=x•(
| 5 |
| x |
| 2 |
| 1 |
| 2 |
| 5 |
=-
| 1 |
| 2 |
| 5 |
| 5 |
| 2 |
当x=
| 5 |
| 5 |
| ||
| 2 |
∴AD=
| AG2+GD2 |
| 5 |
| 2 |
∴OD=
| 3 |
| 2 |
| 3 |
| 2 |
解法二:设DE=x,

∵AC=
| 5 |
| 5 |
∴GC=x,AG=
| 5 |
∴GD=2
| 5 |
∴S矩形DEFG=x•(2
| 5 |
| 5 |
| ||
| 2 |
| 5 |
| 2 |
∴当x=
| ||
| 2 |
∴GD=
| 5 |
| ||
| 2 |
∴AD=
| AG2+GD2 |
| 5 |
| 2 |
∴OD=
| 3 |
| 2 |
∴D(
| 3 |
| 2 |
综上所述:当矩形两个顶点在AB上时,坐标分别为(-
| 1 |
| 2 |
当矩形一个顶点在AB上时,坐标为(
| 3 |
| 2 |

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
 正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.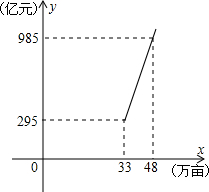 用地总量x(万亩)之间存在着如图所示的一次函数关系.
用地总量x(万亩)之间存在着如图所示的一次函数关系.