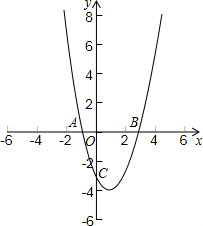��Ŀ����
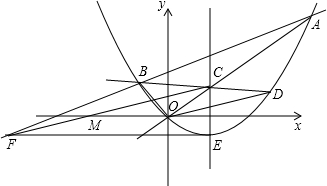
���ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ����A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬��֪��D������Ϊ��0��-3����ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��
��1�������������Բ�������߲��ֵĽ���ʽ����д���Ա�����ȡֵ��Χ��
��2�������Խ���һ�룬�����������������D�ġ���Բ�����ߵĽ���ʽ��
��3�����ֱ��x=m���߶�OB���ƶ�����x���ڵ�D�����������ڵ�E����BD�ڵ�F������DE��BE�������⡰�Ƿ���������ĵ�E��ʹ��BDE��������С��ͬѧ��Ϊ������EΪ�����ߵĶ���ʱ����BDE�����������Ĺ۵��Ƿ� ��ȷ�������ļ��⣬����BDE������������ֵ�������m��ֵ�Լ���E�����꣮
��ȷ�������ļ��⣬����BDE������������ֵ�������m��ֵ�Լ���E�����꣮
��1�������������Բ�������߲��ֵĽ���ʽ����д���Ա�����ȡֵ��Χ��
��2�������Խ���һ�룬�����������������D�ġ���Բ�����ߵĽ���ʽ��
��3�����ֱ��x=m���߶�OB���ƶ�����x���ڵ�D�����������ڵ�E����BD�ڵ�F������DE��BE�������⡰�Ƿ���������ĵ�E��ʹ��BDE��������С��ͬѧ��Ϊ������EΪ�����ߵĶ���ʱ����BDE�����������Ĺ۵��Ƿ�
 ��ȷ�������ļ��⣬����BDE������������ֵ�������m��ֵ�Լ���E�����꣮
��ȷ�������ļ��⣬����BDE������������ֵ�������m��ֵ�Լ���E�����꣮��1����������ߵĽ���ʽΪy=ax2+bx+c��
��������֪A��B��D�������ֱ��ǣ�-1��0������3��0������0��-3����
��������
��
���c=-3��a=1��b=-2��
�ࡰ��Բ�������߲��ֵĽ���ʽΪy=x2-2x-3��-1��x��3����
��2�������D��0��-3���ġ���Բ�����ߵĽ���ʽΪy=kx-3��
������������߲��ֵĽ���ʽΪy=x2-2x-3��
kx-3=x2-2x-3����x2-��2+k��x=0��
�ߡ�=��2+k��2=0��
��k=-2��
�����D��0��-3���ġ���Բ�����ߵĽ���ʽΪy=-2x-3��
��3��������֪B��D�������ֱ��ǣ�3��0������0��-3����
��ֱ��BD�Ľ���ʽΪy=x-3��
�ߵ�FΪֱ��x=m��ֱ��BD�Ľ��㣬��EΪֱ��x=m��������y=x2-2x-3�Ľ��㣬
���F��������m��m-3������E��������m��m2-2m-3����
��S��BDE=S��BDF+S��DEF=
��EF��OD+
��EF��DB��
=
��EF��OB��
=
[m-3-(m2-2m-3)]��3��
=
(3m-m2)��
=-
(m-
)2+
��
�֡�0��m��3��
�൱m=
��S��BDEȡ���ֵ
����E��������
��-
����
�������ߵĶ���Ϊ��1��-4����
��С��ͬѧ��Ϊ������EΪ�����ߵĶ���ʱ����BDE�������������Ĺ۵��Ǵ���ģ�
�𣺣�1������Բ�������߲��ֵĽ���ʽΪy=x2-2x-3��-1��x��3����
��2������D��0��-3���ġ���Բ�����ߵĽ���ʽΪy=-2x-3��
��3�����������ĵ�E������Ϊ��
��-
����ʹ��BDE��������Ϊ
��С��ͬѧ��Ϊ������EΪ�����ߵĶ���ʱ����BDE�������������Ĺ۵��Ǵ���ģ�
��������֪A��B��D�������ֱ��ǣ�-1��0������3��0������0��-3����
��������
|
���c=-3��a=1��b=-2��
�ࡰ��Բ�������߲��ֵĽ���ʽΪy=x2-2x-3��-1��x��3����
��2�������D��0��-3���ġ���Բ�����ߵĽ���ʽΪy=kx-3��
������������߲��ֵĽ���ʽΪy=x2-2x-3��
kx-3=x2-2x-3����x2-��2+k��x=0��
�ߡ�=��2+k��2=0��
��k=-2��
�����D��0��-3���ġ���Բ�����ߵĽ���ʽΪy=-2x-3��
��3��������֪B��D�������ֱ��ǣ�3��0������0��-3����
��ֱ��BD�Ľ���ʽΪy=x-3��
�ߵ�FΪֱ��x=m��ֱ��BD�Ľ��㣬��EΪֱ��x=m��������y=x2-2x-3�Ľ��㣬
���F��������m��m-3������E��������m��m2-2m-3����
��S��BDE=S��BDF+S��DEF=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
�֡�0��m��3��
�൱m=
| 3 |
| 2 |
| 27 |
| 8 |
| 3 |
| 2 |
| 9 |
| 4 |
�������ߵĶ���Ϊ��1��-4����
��С��ͬѧ��Ϊ������EΪ�����ߵĶ���ʱ����BDE�������������Ĺ۵��Ǵ���ģ�
�𣺣�1������Բ�������߲��ֵĽ���ʽΪy=x2-2x-3��-1��x��3����
��2������D��0��-3���ġ���Բ�����ߵĽ���ʽΪy=-2x-3��
��3�����������ĵ�E������Ϊ��
| 3 |
| 2 |
| 15 |
| 4 |
| 27 |
| 8 |

��ϰ��ϵ�д�
�����Ŀ