题目内容
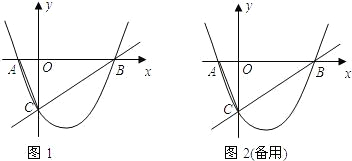
抛物线y=ax2+bx+c(a>0)经过点A(-3
,0),B(
,0)与y轴交于点C,设抛物线的顶点为D,在△BCD中,边CD的高为h.
(1)若c=ka,求系数k的值;
(2)当∠ACB=90°,求a及h的值;
(3)当∠ACB≥90°时,经过探究、猜想请你直接写出h的取值范围.
(不要求书写探究、猜想的过程)

| 3 |
| 3 |
(1)若c=ka,求系数k的值;
(2)当∠ACB=90°,求a及h的值;
(3)当∠ACB≥90°时,经过探究、猜想请你直接写出h的取值范围.
(不要求书写探究、猜想的过程)

(1)因为A(-3
,0),B(
,0)在抛物线y=ax2+bx+c(a>0)上,
所以有,y=a(x+3
)(x-
)=a(x2+2
x-9),
又因为c=-9a
所以k=-9.
(2)由于∠ACB=90°时,
∵OC⊥AB,
∴∠AOC=∠BOC=90°.
可得∠ACO=∠OBC.
∴△AOC∽△COB.
∴
=
,
即OC2=OA•OB=3
×
=9.
∴OC=3.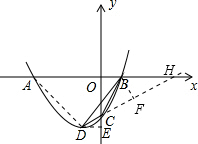
∵C(0-3),由(1)知-9a,
∴a=
.
过D作DE⊥OC交y轴于点E,延长DC交x轴于点H,过B作BF⊥CH于点F.
即BF是边DC的高h.
因为D是抛物线的顶点,
所以D(-
,-4),
故OE=4,又OC=3,可得CE=1,DE=
.
易证△HCO∽△DCE,有
=
=
=3,
故OH=3DE=3
,BH=OH-OB=2
.
由于∠COH=90°,OC=3,OH=3
,由勾股定理知CH=6,有∠OHC=30°,
又因为在Rt△BHF中,BH=2
,
所以BF=
,即h=
.
(3)当∠ACB≥90°时,猜想0<h≤
.
| 3 |
| 3 |
所以有,y=a(x+3
| 3 |
| 3 |
| 3 |
又因为c=-9a
所以k=-9.
(2)由于∠ACB=90°时,
∵OC⊥AB,
∴∠AOC=∠BOC=90°.
可得∠ACO=∠OBC.
∴△AOC∽△COB.
∴
| AO |
| OC |
| OC |
| OB |
即OC2=OA•OB=3
| 3 |
| 3 |
∴OC=3.

∵C(0-3),由(1)知-9a,
∴a=
| 1 |
| 3 |
过D作DE⊥OC交y轴于点E,延长DC交x轴于点H,过B作BF⊥CH于点F.
即BF是边DC的高h.
因为D是抛物线的顶点,
所以D(-
| 3 |
故OE=4,又OC=3,可得CE=1,DE=
| 3 |
易证△HCO∽△DCE,有
| HO |
| DE |
| CO |
| EC |
| 3 |
| 1 |
故OH=3DE=3
| 3 |
| 3 |
由于∠COH=90°,OC=3,OH=3
| 3 |
又因为在Rt△BHF中,BH=2
| 3 |
所以BF=
| 3 |
| 3 |
(3)当∠ACB≥90°时,猜想0<h≤
| 3 |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目